Синтез оптимальных наблюдателей переменных состояния нелинейных объектов управления

Глава 2. СИНТЕЗ ОПТИМАЛЬНЫХ НАБЛЮДАТЕЛЕЙ

ПЕРЕМЕННЫХ СОСТОЯНИЯ НЕЛИНЕЙНЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ

2.1. Априорная модель системы управления

2.1.1. Априорная модель возмущающих воздействий

Известно, что возмущающие воздействия , , образующие вектор , являются ограниченными функциями времени. При этом выполняются ограничения

, .

(2.1.1)

В скользящем временном окне, протяженностью , изменение во времени математических ожиданий возмущающих воздействий можно описать, например, с помощью В‑сплайнов [30], [55]. Тогда с учетом ограничений (2.1.1) математическую модель возмущающих воздействий можно описать следующими уравнениями:

,  ,

(2.1.2)

, ,

(2.1.3)

где 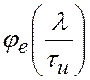 – известные финитные функции;  – коэффициенты сплайнов, значения которых определяют методом наименьших квадратов (МНК) в каждом временном окне с использованием апостериорных оценок  возмущающих воздействий в моменты времени 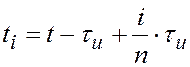, ;  -  отклонение текущих значений возмущающего воздействия  от заданной сплайнами линии регрессии (погрешность аппроксимации), которое можно считать случайным процессом с нулевым средним значением;  - текущий момент времени.

В частности, при использовании В-сплайнов первого порядка

,

.

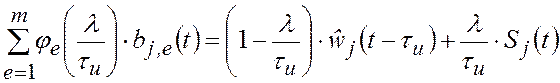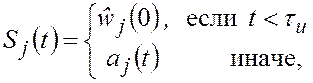
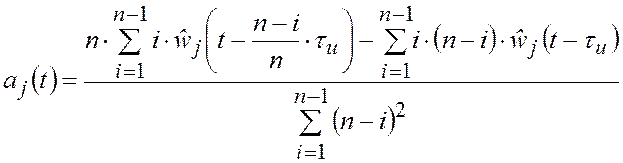Кусочно-непрерывные функции, содержащиеся в правых частях уравнения (2.1.2), можно аппроксимировать с любой требуемой точностью аналитическими функциями

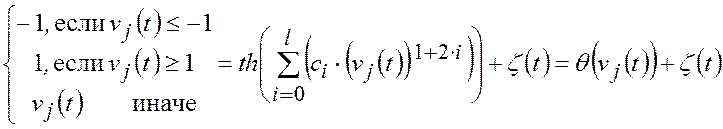
подбором параметров , где  - допустимая погрешность аппроксимации. График такой функции при ,  и  приведен на рисунке 2.1. Поэтому с точностью до погрешности аппроксимации  неравенства (2.1.1) можно заменить нелинейным уравнением

.

(2.1.4)

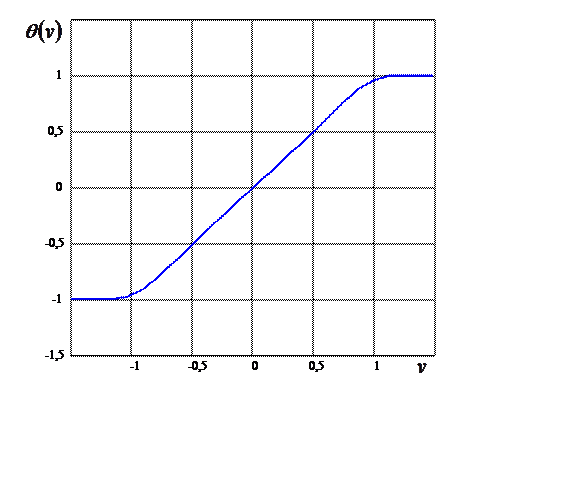
Рис. 2.1. График функции (2.1.4) с параметрами: ,  , ,

В зависимости от имеющейся априорной информации можно применять различные математические модели генератора случайных процессов . В частности, можно построить модель генератора цветных шумов (ГЦШ) в пространстве состояний, если известны их корреляционные функции  [31].

В дальнейшем предполагается, что порядок В-сплайнов и величина временного окна  выбраны таким образом, что корреляционные функции случайных процессов  с достаточной точностью можно аппроксимировать формулой

, ,

(2.1.5)

где  - дисперсия случайного процесса .

Из теории случайных процессов следует [21], что в текущем временном окне корреляционную функцию случайного процесса  можно вычислить по формуле 

,

где  - переходная функция генератора случайного процесса .

Непосредственными вычислениями можно показать, что переходную функцию

(2.1.6)

имеет генератор цветного шума

,

(2.1.7)

где  – белый шум с нулевым средним значением и интенсивностью

.

(2.1.8)

Из (2.1.3) и (2.1.7) следуют равенства

.

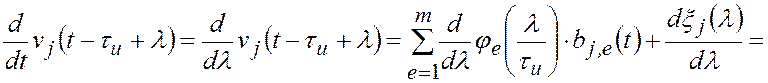
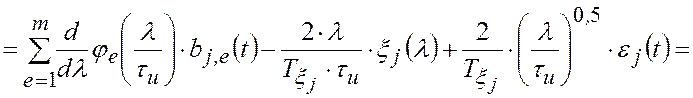
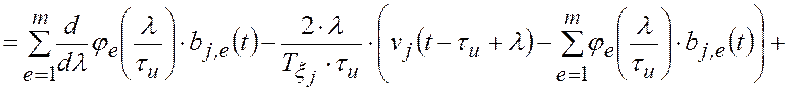
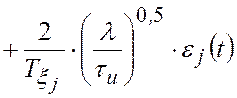Поэтому при  получим априорную модель генератора возмущающих воздействий в виде линейного дифференциального уравнения

(2.1.9)

с начальными условиями

,     ,

(2.1.10)

где  – вектор, образованный из белых шумов ;

;

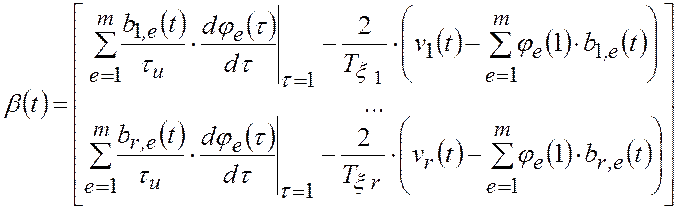 – диагональная матрица с элементами .

Таким образом, априорная модель возмущающих воздействий (рис. 2.2) представляет собой последовательное соединение ГЦШ (2.1.8)-(2.1.10) и нелинейного преобразователя (НП) (2.1.4). Такая система формирует возмущающие воздействия  из белых шумов, объединенных в вектор .

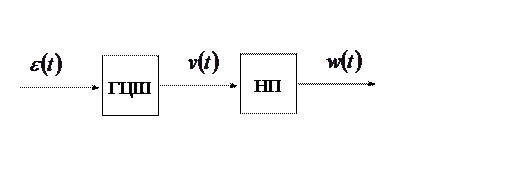
Рис. 2.2. Априорная модель генератора возмущающих воздействий

Очевидно, что при составлении априорной модели возмущающих воздействий можно применять и другие способы аппроксимации.

2.1.2. Априорная модель допустимых управляющих воздействий

Предполагается, что управляющие воздействия ,  образую-щие вектор , принадлежат множеству непрерывных функций времени. При этом управляющие воздействия ограничены неравенствами

, .

(2.1.11)

В скользящем временном окне, протяженностью , изменение во времени математических ожиданий управляющих воздействий можно описать с помощью В‑сплайнов.

Предполагается, что отклонения допустимых управляющих воздействий от линий регрессии, заданных В‑сплайнами, являются случайными процессами с нулевыми средними значениями и корреляционными функциями

.

(2.1.12)

 Тогда, как это было показано в разделе 2.1.1, множество допустимых управляющих воздействий (2.1.11), (2.1.12) можно задать уравнениями

,

(2.1.13)

(2.1.14)

с начальными условиями

,      ,

(2.1.15)

где  – вектор параметров, значения которых определяют методом наименьших квадратов (МНК) в каждом временном окне с использованием апостериорных оценок  управляющих воздействий в моменты времени 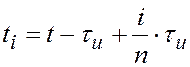, ;   – вектор, образованный белыми шумами  с нулевыми средними значениями и матрицей интенсивностей .

2.1.3. Априорная модель состояния объекта управления

Предполагается, что процессы, протекающие в объекте управления, описывают нелинейным уравнением состояния

(2.1.16)

 с начальными условиями

,     ,

(2.1.17)

где  – вектор переменных состояния  объекта;  – вектор известных функций, имеющих ограниченные производные своих аргументов;  - вектор известных оценок значений переменных состояния в начальный момент времени, которые являются случайными величинами с нормальным законом распределения вероятности.