Синтез оптимальных наблюдателей переменных состояния нелинейных объектов управления, страница 5

Функция стоимости ПИД-наблюдателя переменных состояния объекта управления с произвольными шумами. Из формулы (2.2.8) следует, что задача максимизации условной плотности  эквивалентна задаче минимизации квадратичной функции стоимости

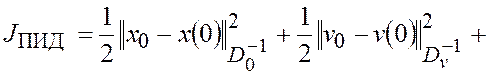
(2.2.11)

по переменным ,  и  при ограничениях (2.2.1), (2.1.4) и (2.1.27).

Если функции распределения погрешностей аппроксимации  и погрешностей измерений  отличны от гауссовских, либо неизвестны, то выражение (2.2.11) является функцией стоимости обобщенного метода наименьших квадратов, где  и  - матрицы дисперсий погрешностей задания переменных состояния  и возмущающих воздействий  в начальный момент времени;  и  - положительно определенные матрицы весовых коэффициентов.

Оценки матриц весовых коэффициентов  и  можно вычислять по формулам (2.1.24) и (2.1.8) соответственно.

Если начальные значения переменных состояния  и возмущающих воздействий  являются гауссовскими случайными величинами, а погрешности аппроксимации  и погрешности измерений  - гауссовские цветные шумы с нулевыми средними значениями и корреляционными функциями (2.1.5) и (2.1.22), то оценки переменных состояния по критерию МНК (2.2.11) оптимальны и по критерию МАВ (2.2.8).

Функция стоимости (2.2.11) содержит взвешенную сумму погрешностей оценивания выходных сигналов измерительных устройств  (пропорциональная (П) часть функции стоимости ), взвешенную сумму средних значений этих погрешностей оценивания  (2.2.10) (интегральная (И) часть функции стоимости ) и взвешенную сумму производных по времени этих же погрешностей оценивания (дифференциальная (Д) часть функции стоимости ). Поэтому выражение (2.2.11) будем называть функцией стоимости ПИД-наблюдателя обобщенного МНК для нелинейного объекта управления (2.2.1)-(2.2.3), (2.1.4), (2.1.27) с произвольными шумами.

2.3.Наблюдатели переменных состояния нелинейных объектов

2.3.1. ПИ-наблюдатели переменных состояния

нелинейных объектов

ПИ-наблюдатель переменных состояния, оптимальный по критерию МАВ. Решение задачи синтеза оптимального по критерию МАВ (2.2.7) наблюдателя переменных состояния нелинейного объекта управления (2.2.1), (2.2.2) с измерительными устройствами  (2.2.3), (2.1.21) определяет следующая теорема.

Теорема 1. Пусть управляемый и наблюдаемый объект управления имеет нелинейное уравнение состояния

(2.3.1)

с начальными условиями

,

(2.3.2)

и на этот объект действуют возмущающие воздействия , изменение во времени которых описывают с помощью В-сплайнов уравнениями

,

(2.3.3)

; ,

(2.3.4)

с начальными условиями

,       ,

(2.3.5)

где  - вектор погрешностей аппроксимации  с нулевыми средними значениями и корреляционными функциями

,  .

(2.3.6)

Пусть вектор выходных сигналов  измерительных устройств и переменные состояния   связаны нелинейным  уравнением

,

(2.3.7)

где  - вектор средних значений погрешностей измерений;  - вектор случайных составляющих погрешностей измерений. Пусть начальные значения  и  являются гауссовскими случайными величинами, а погрешности измерений  - гауссовские белые шумы с нулевыми средними значениями и матрицей интенсивнос- тей .

Тогда оценку  переменных состояния  , оптимальную по критерию максимума апостериорной вероятности (2.2.7), формирует следующая динамическая система (ПИ-наблюдатель переменных состояния:

,

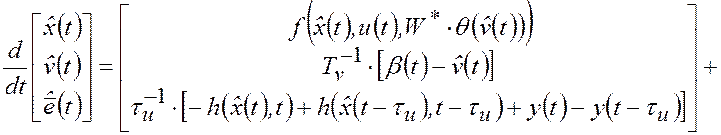
(2.3.8)

,

(2.3.9)

(2.3.10)

с начальными  условиями

,  ,    ,   ,

(2.3.11)

где

;

(2.3.12)

;;

(2.3.13)

.

(2.3.14)

Для доказательства теоремы 1 введем по формулам (2.2.10) новую переменную  - вектор средних по времени значений погрешностей оценивания  выходных сигналов измерительных устройств .

Уравнение (2.2.10) можно заменить эквивалентным дифференциальным уравнением

(2.3.15)

при условии, что , если .