Узлы и механизмы полиграфического оборудования. Зубчатые механизмы. Прочностные расчеты зубчатых передач, страница 7

При выбранных передаточных отношениях числа зубьев шестерен можно назначить в соответствии с требованиями к механизму. Это достаточно сложная и многовариантная задача, которая достаточно корректно решается только с помощью ЭВМ. Критериями оптимизации служат габаритные ограничения, минимизация массы, приведенного момента инерции или угловой погрешности.

Основная теорема зацепления. Условие нормальной работы зубчатой передачи с круглыми колесами – обеспечение постоянного передаточного отношения. Это возможно лишь при определенном очертании сопряженных профилей зубьев шестерни и колеса. Пусть, например, шестерня 1 и колесо 2 находятся в зацеплении (рис.2.3, а);  и  - радиусы  их начальных окружностей. Линии NN и KK – нормаль и касательная в точке С соприкосновения профилей зубьев шестерни и колеса: u_С1 ^ О₁С и  u_С2 ^ О₂С- скорости точки С, принадлежащей зубу шестерни 1 и зубу колеса 2  соответственно.

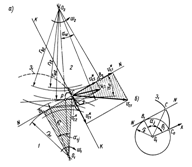Рисунок 2.3 – К выводу основной теоремы зацепления

Суть основной теоремы зацепления состоит в том, что для обеспечения условия сопряженные профили зубьев должны быть очерчены такими кривыми, у которых нормаль NN в любой точке С взаимного касания зубьев (рис. 2.3, а) всегда проходят через постоянную точку Р на линии центров колес О₁О₂. Докажем эту теорему.

Векторы  и  могут быть разложены на составляющие по линиям NN и KK:

; .

Очевидно, что нормальное зацепление возможно лишь при условии . В противном случае зуб шестерни либо врежется в зуб колеса, либо отстанет от него. Из подобных треугольников (на рис.2.3, а они заштрихованы) следует, что

,

откуда . Аналогично, . Учитывая равенство , можно записать

.

Так как прямоугольные треугольники  и  подобны, то окончательно получаем

/=i_12.

Следовательно, если точка Р пересечения нормали NN с линией центров не меняет своего положения, то i₁₂ = const, что и требовалось доказать.

Постоянную точку Р на линии центров колеса принято называть полюсом зацепления. Эта точка определяет радиусы начальных окружностей r_w1 и r_w2.

                Теореме зацепления удовлетворяют профили зубьев, очерченные различными кривыми; наиболее простой и удобный по технологии нарезания зубьев – эвольвентный профиль, впервые предложенный Л. Эйлером.

В основной теореме зубья рассматриваются как абсолютно жесткие, т.е. их деформации не учитываются. Для малонагруженных передач деформации зубьев меньше погрешностей изготовления и требования теоремы полностью отвечают практике. Однако синтез относительно высоконагруженных зацеплений выполняют с учетом деформации профилей; в результате получают профили, не удовлетворяющие основной теореме, но дающие при расчетной нагрузке оптимальные по ряду параметров передач.