Узлы и механизмы полиграфического оборудования. Зубчатые механизмы. Прочностные расчеты зубчатых передач, страница 12

                3.3 Расчет зубьев на изгиб

Цель расчета обеспечить выносливость зуба при изгибе, то есть предотвратить его усталостный излом.

В первом приближении зуб рассматривают как балку, защемленную одним концом. Наиболее опасно, когда нагрузка F_n действует на вершину зуба, что соответствует моменту начала или конца защемления. Окружное усилие F_t перпендикулярно оси зуба и вызывает изгиб, радиальная составляющая F_r направлена вдоль оси зуба и сжимает зуб (рис. 3.2).

 

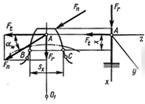
Рисунок 3.2 – Схема действия сил

При совместном действии этих деформаций, трещины возникают на растянутой стороне зуба; расчетное напряжение в сечении на расстоянии х от точки А.

,

где M_N(x)=F_t*x– изгибающий момент в рассматриваемом сечении;

W_y(x)=b*S_x²/6 - осевой момент сопротивления сечения прямоугольника в плане;

b - ширина зубчатого венца;

S_x - переменная по высоте толщина зуба;

b*S_x - площадь сечения зуба.

,

где Т – крутящий момент на данном звене, Н*мм;

d - диаметр делительной окружности.

Окончательный вид формулы для шестерни

,                         для колеса

;

                где d₁=mz₁/cosβ – делительный диаметр (b - делительный угол наклона зубьев);

b - рабочая ширина зубчатого венца;

Y_F - коэффициент, учитывающий влияние формы зуба;

Y_β - для косозубых передач равен 0,7.

4 Точность зубчатых передач. Конструктивные и технологические особенности

4.1   Параметры точности

Точность преобразования движения зубчатыми передачами зависит как от точности выполнения геометрических элементов передачи, так и относительного их расположения. Кроме того, на точность зубчатого механизма влияют упругие деформации зубьев, валов, опор и других элементов передачи.

Качество работы зубчатых передач зависит в основном от следующих факторов[2]:

- кинематической точности передачи, которая характеризует постоянство передаточного отношения за один оборот ведущего и ведомого колес; кинематическая погрешность одного колеса ∆F_Σ   (рис. 4.1) представляет собой наибольшее в течение одного оборота отклонение δ_φ угла поворота φ зубчатого колеса при зацеплении с точным колесом;

Рисунок 4.1 – Параметры точности зубчатого колеса

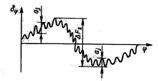
- плавности хода передачи, которая характеризует постоянство передаточного отношения в пределах поворота колеса на один зуб (на угловой шаг); плавность хода оценивается циклической погрешностью ∆F=(1/n)åa_j, многократно повторяющейся за оборот колеса (рис. 4.1);

- степени контакта сопряженных зубьев колес, определяющей полноту прилегания рабочих поверхностей зубьев.

Для сравнительной оценки точности изготовления зубчатых колес и  сборки передачи ГОСТ 9178 – 72 (для 0,1≤m<1 мм) и 1643 – 72 (для m≥1 мм) предусмотрено 12 степеней точности, по которым определяют допуски и отклонения. Первые три степени будут использоваться в перспективе. Степени 4 и 5 – особо точные зубчатые колеса, к которым предъявляют высокие требования по постоянству передаточного отношения и плавности хода. Применение этих степеней точности должно быть обосновано соответствующим расчетом и разрешено руководителем предприятия. Степень 6 – высокоточные отсчетные зубчатые колеса, углы поворота которых соответствуют отсчетным значениям с большой ценой деления. Кроме того, эту степень точности используют для высокоскоростных передач при окружных скоростях более 8 м/с. Степень 7 – точные колеса, предназначенные для плавной работы при окружных скоростях 5…8 м/с. Наиболее часто назначают 8-ю степень – это колеса средней точности, удовлетворительно работающие при окружной скорости      до 5 м/с.