Грузовые перевозки: Сборник методических указаний к практическим занятиям, страница 8

4.  Дальнейшее решение связано с подготовкой специально поставленной транспортной задачи, в которой минимизируется сумма произведений порожних ездок на длины соответствующих холостых пробегов. При этом, в соответствии с терминологией классической транспортной задачи, пункты   1, …, i, …, n   будут поставщиками порожних ездок, а пункты 0 (центральный склад) и  АТП – потребителями этих ездок. Причем  АТП  будет потребителем последней порожней ездки в каждом маршруте (количество таких ездок равно числу автомобилей А, возвращающихся после рабочего дня в АТП ). После этого легко заполнить таблицу с исходными данными транспортной задачи (табл. 1):

Таблица 1

5.  Решается такая транспортная задача любым из известных методов, например, методом потенциалов. В результате определяется оптимальный план распределения порожних ездок между пунктами дорожной сети. Ездки, попавшие в столбец  АТП (например, Х_1,АТП, Х_i,АТП  в табл.2),определяют последние пункты маршрутов (в нашем случае это пункты 1 и i), из которых автомобили должны возвращаться в АТП.

Таблица 2

Величины  X_1,АТПи   X_i,АТП   определяют количество маршрутов, последние ездки которых  …1 – АТП  и  …i – АТП соответственно. Ездки, попавшие только в столбец  0  (в нашем случае X_n,0), говорят о том, что из соответствующего пункта (в нашем случае из пункта n) нецелесообразно возвращаться в АТП.

6.  Наконец, строятся маршруты движения каждого автомобиля, например:

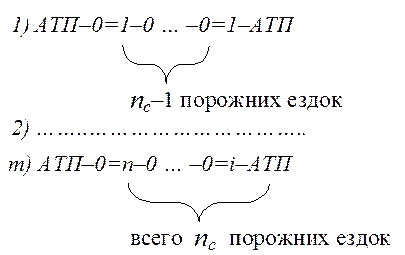
7.  Затем определяют холостой, груженый и полный пробег каждого автомобиля в отдельности и в целом по всем автомобилям.

Порядок выполнения работы

9.  Изучить теоретическую часть работы.

10.  Сравнить между собой два варианта организации перевозок однородных грузов из центрального склада клиентам маятниковыми маршрутами. Дорожная сеть показана в виде графа на рис. 1.

Студент в соответствии со своим номером в журнале должен выбрать вариант исходных данных из таблицы 1.

Таблица 1

№ по журналу	Вариант	№ по журналу	Вариант	№ по журналу	Вариант
1	1-1-1	10	2-1-1	19	3-1-1
2	1-1-2	11	2-1-2	20	3-1-2
3	1-1-3	12	2-1-3	21	3-1-3
4	1-2-1	13	2-2-1	22	3-2-1
5	1-2-2	14	2-2-2	23	3-2-2
6	1-2-3	15	2-2-3	24	3-2-3
7	1-3-1	16	2-3-1	25	3-3-1
8	1-3-2	17	2-3-2	26	3-3-2
9	1-3-3	18	2-3-3	27	3-3-3

Конкретные исходные данные выбираются из таблиц 2, 3, 4 и 5 в зависимости от комбинации цифр варианта.