Грузовые перевозки: Сборник методических указаний к практическим занятиям, страница 5

Цель занятия: освоение методов и приемов закрепления клиентуры за АТП путем использования "транспортной задачи"

Теоретические сведения

Вариант 3.

Если АТП имеют разнотипный подвижной состав с различной выработкой на тонну грузоподъемности, то задача закрепления клиентуры за АТП в этом общем случае математически формулируется следующим образом.

Введем обозначения:

число клиентов;

количество груза, которое требуется доставить  j-му клиенту (), т.;

число типов подвижного состава;

количество единиц подвижного состава i-го типа ();

грузоподъемность автомобиля i-го типа, т.;

производительность единицы подвижного состава i-го типа при работе у j-го клиента, т.;

себестоимость перевозки 1т груза автомобилем i-го типа у j-го клиента, руб.;

прибыль, получаемая при перевозке 1т груза автомобилем i-го типа  у  j-го клиента, руб.;

количество автомобилей i-го типа, работающих у j-го клиента.

Составить план использования автомобилей    при условиях:

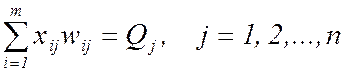                               (12)

(каждому клиенту груз должен быть доставлен полностью);

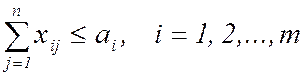                                    (13)

(число используемых на перевозках автомобилей каждого типа не может превышать наличного количества);

                        (14)

(переменные не могут быть отрицательными).

Выбор показателя эффективности решения системы (12)-(14) имеет весьма важное значение. Обычно используют один из следующих, наиболее распространенных, показателей:

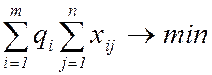                                           (15)

(суммарная грузоподъемность используемого на перевозках подвижного состава должна быть минимальной);

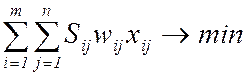                                     (16)

(суммарные затраты, связанные с перевозками грузов, должны быть минимальными);

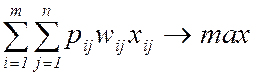                                     (17)

(прибыль, получаемая в результате выполнения перевозок, должна быть максимальной).

Существуют и другие критерии.

Таким образом, задача закрепления клиентуры за АТП с разнотипным подвижным составом, имеющим разную производительность на тонну грузоподъемности, сводится к решению системы (12)-(14) по критерию (15), (16) или (17). Сформулированная задача известна в литературе под названием обобщенной транспортной задачи линейного программирования (задача).

Задача закрепления клиентуры за АТП может решаться с различной периодичностью (ежегодно, ежеквартально, ежемесячно и т.д.) в зависимости от конкретных условий.

Алгоритм решения

Вариант 3.

Задача (12)-(14) с критерием (15), (16) или (17) также может быть решена, например, методом потенциалов, но для этого необходимо предварительно выполнить следующее:

1.  Введем дополнительный столбец (фиктивный потребитель) с тем, чтобы в условиях (13) заменить неравенство на равенство. Задача при этом принимает вид:

 ,

 ,

 ,

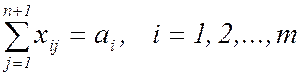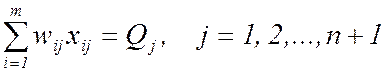где  ,

 ,

а значение  пока не определено и меняется на каждой итерации;

2.  Целевую функцию (15), (16) или (17) приводим к виду

 ,

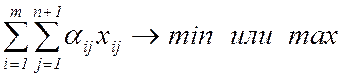где ,       или  соответственно для (15), (16) или (17). Для определенности далее в качестве критерия примем (15).

3.  Определяем начальное базисное решение

 

по следующему правилу:

a)  вычисляем элементы матрицы

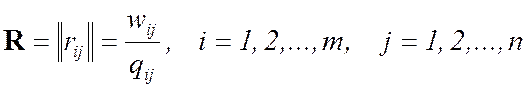
b)  выбираем  так, чтобы

,

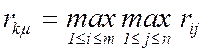c)  полагаем

 ,

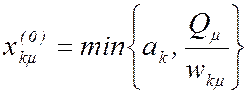d)  полагаем

;

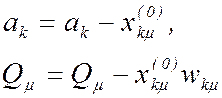e)  исключаем из дальнейшего рассмотрения k-ю строку (если  ) и μ-й столбец (если  );

f)  проверяем все ли  или все  равны нулю. Если нет, то переход к п.п. "b" алгоритма, в противном случае – к п.п. "g";

g)  полагаем

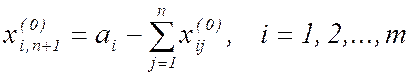
На этом определение начального базисного решения заканчивается.

4.  Определяем потенциалы строк  и столбцов  по следующему правилу:

 ,

отсюда

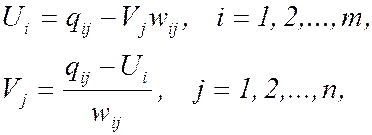
а потенциал фиктивного (n+1)-го столбца всегда принимаем равным нулю, т.е.  .

5.  Вычисляем характеристику

Если  , то найденное решение оптимально и алгоритм на этом свою работу заканчивает.

Если же хотя бы для одного  то план не оптимален, его можно улучшить путем введения в базис элемента с индексом  . При наличии нескольких элементов с отрицательными характеристиками  в базис рекомендуется вводить элемент, у которого отрицательная характеристика максимальна по абсолютной величине.