Защита отчета на следующем занятии
Практическое занятие № 2 (часть 1)
(6 часов)
Изучение методов оптимизации закрепления
клиентуры за АТП
Цель занятия: освоение методов и приемов закрепления клиентуры за АТП путем использования "транспортной задачи"
Решение задачи "Оптимальное закрепление клиентуры за автотранспортными предприятиями" позволяет значительно сократить непроизводительные (нулевые) пробеги автомобилей, повысить производительность работы транспорта и снизить себестоимость перевозок.
Это первая автотранспортная задача, для которой использовались экономико-математические методы.
В настоящее время существуют три варианта постановки задачи оптимального закрепления клиентуры за АТП.
Вариант 1.
В автотранспортных предприятиях (или филиалах одного предприятия)
![]() имеется соответственно
имеется соответственно ![]() автомобилей одинаковой грузоподъемности
автомобилей одинаковой грузоподъемности ![]() . Клиентам
. Клиентам ![]()
![]() нужно подавать
нужно подавать ![]() автомобилей.
Расстояния между всеми пунктами известны (задана матрица нулевых пробегов
автомобилей.
Расстояния между всеми пунктами известны (задана матрица нулевых пробегов ![]() ). Необходимо закрепить клиентуру за
автотранспортными предприятиями так, чтобы суммарный нулевой пробег был
минимальным.
). Необходимо закрепить клиентуру за
автотранспортными предприятиями так, чтобы суммарный нулевой пробег был
минимальным.
Математически задача формулируется так:
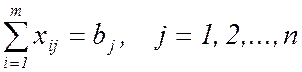 (1)
(1)
(потребность каждого клиента в автомобилях удовлетворяется полностью);
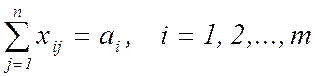 (2)
(2)
(каждое автотранспортное предприятие выпускает на линии перевозок весь имеющийся подвижной состав);
![]() (3)
(3)
(переменные ![]() ,
означающие количество автомобилей i-го автотранспортного
предприятия закрепленных за j-м клиентом, не могут быть отрицательными);
,
означающие количество автомобилей i-го автотранспортного
предприятия закрепленных за j-м клиентом, не могут быть отрицательными);
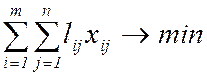 (4)
(4)
(суммарный нулевой пробег автомобилей должен быть минимальным).
Сформулированная задача представляет собой транспортную задачу линейного программирования в классической постановке. Как известно, для ее разрешимости должно быть выполнено условие баланса между спросом и предложением
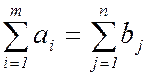
Если это условие не соблюдается, то вводят либо фиктивного клиента, либо фиктивное автопредприятие с фиктивными нулевыми пробегами (равны 0).
Решение транспортной задачи выполняют, например, методом потенциалов или любым другим известным методом.
Вариант 2.
В отличие от предыдущего варианта в данном случае считается, что АТП располагают различным по грузоподъемности подвижным составом, который, однако, является взаимозаменяемым, т.е. может использоваться любыми клиентами.
Автомобили различных марок имеют разную грузоподъемность и в этом
смысле не равны между собой: на заданный объем перевозок клиенту требуется
различное в зависимости от грузоподъемности количество автомобилей. Поэтому при
решении исходные данные о выпуске автомобилей и потребности в них клиентуры
надо использовать в преобразованном виде – в форме суммарного тоннажа
подвижного состава. При этом число АТП искусственно увеличивается так, чтобы в
каждом автотранспортном предприятии имелись автомобили только одного типа. Этот
прием приводит также к необходимости пересчета расстояний ![]() , используемых в матрице. Для этого нужно
разделить соответствующие расстояния на грузоподъемность автомобилей, которые
будут по ним двигаться.
, используемых в матрице. Для этого нужно
разделить соответствующие расстояния на грузоподъемность автомобилей, которые
будут по ним двигаться.
Кроме того, расходы на один километр пробега у автомобилей различных марок неодинаковы, поэтому критерием оптимальности должен быть не минимум суммарного нулевого пробега, а минимум суммарной стоимости нулевого пробега. Для решения задачи с этим критерием в матрице вместо расстояний нужно записывать стоимость нулевого пробега различных марок автомобилей. Причем эти стоимости необходимо скорректировать так, как было описано выше для расстояний.
Математически задача закрепления клиентуры за АТП с отмеченными особенностями выглядит следующим образом:
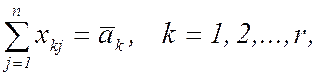 (5)
(5)
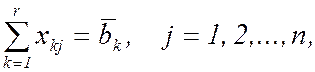 (6)
(6)
![]() , (7)
, (7)
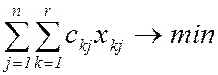 ,
(8)
,
(8)
где
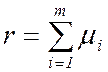 , (9)
, (9)
![]() ,
(10)
,
(10)
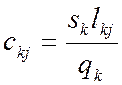 .
(11)
.
(11)
В задаче (5)‑(11) приняты следующие обозначения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.