Курс лекций по дисциплине «Информационно-измерительные системы», страница 35

Эргодический случайный процесс – это стационарный случайный процесс, у которого числовые характеристики определяются усреднением по ансамблю реализации, совпадают с числовыми характеристиками, полученные при одной реализации.

                   

Перед измерением случайного процесса нужно проверить гипотезу о стационарности и эргодичности.

5.15.1 Вероятность пребывания случайной эргодической функции в заданном диапазоне значений

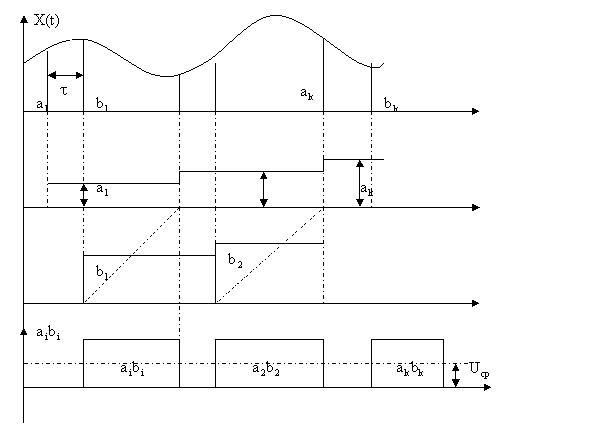
Рассмотрим случайный процесс X(t), где T – время преобразования случайного процесса в дифференциальном коридоре:

        

 

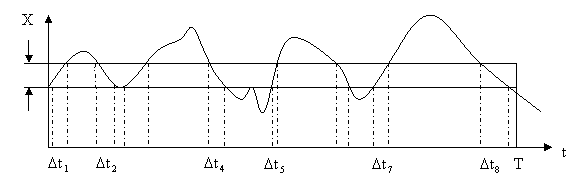
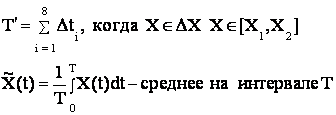Среднестатистическое от среднего по времени равно среднестатистическому.

      Выполним статистическое усреднение:

                     .

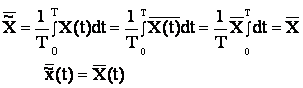Рассмотрим функцию:  ,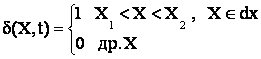

где - стационарна и случайна.

      Ее среднестатистическое:

           

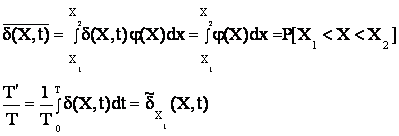
       Усреднив статистическое, получим:

 .

Вывод: среднестатистическое относительно время пребывания в заданном интервале значений, есть вероятность его пребывания в этом диапазоне.

6 ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛЬНОЙ ПОМЕХОУСТОЙЧИВОСТИ

Схема канала передатчика – приемника: 

                   

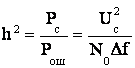
         При передачи «1» и «0» на фоне шумов мы рассматриваем поэлементный прием. Если обозначить  сигнал посылки как S(t), то получим:

                 

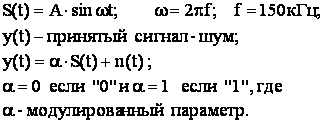
На приемной стороне  мы должны узнать, что передавалось «1» или «0».