Курс лекций по дисциплине «Информационно-измерительные системы», страница 32

5.11.1 Стационарные случайные процессы (ССП)

.

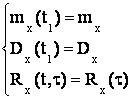5.11.2 Спектральное разложение  ССП

                 

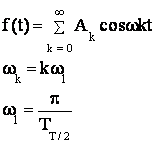
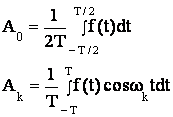
5.12 Разложение в ряд Фурье. Каноническое разложение ССП.

     ,

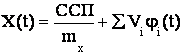где случайная величина     

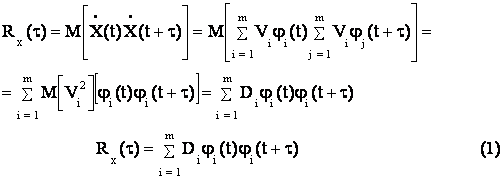
Разложение в ряд Фурье для детерминированной функции, которые имеют постоянную форму. Случайный сигнал неразложим в ряд Фурье, так как он не имеет формы, амплитуды. Хотелось бы иметь аналог разложения в ряд Фурье, если не для самого процесса, то для какой-то его функции.

         Один из русских математиков Пугачев предложил метод канонического разложения.

           

 Каноническое  разложение позволило получить общее выражение для  :        

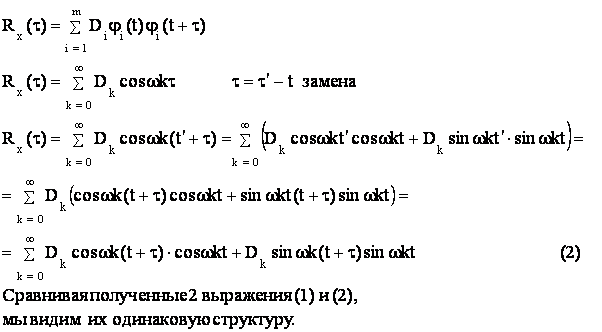
         На основании теоремы, доказанной Пугачевым, случайная функция X(t) может быть представлена каноническим разложением, координатные функции которого совпадают с координатными функциями канонического разложения корреляционной функции этого же процесса X(t) т.о процесс X(t) может быть записан в виде:

                      

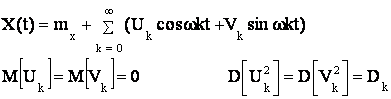
Т.о случайные коэффициенты  должны иметь дисперсию случайных коэффициентов канонического разложения корреляционной функции.

Зная вид разложения корреляционной функции X(t) можно определить координатные функции.

Определим мощность случайной функции  , которая представлена             в каноническом виде: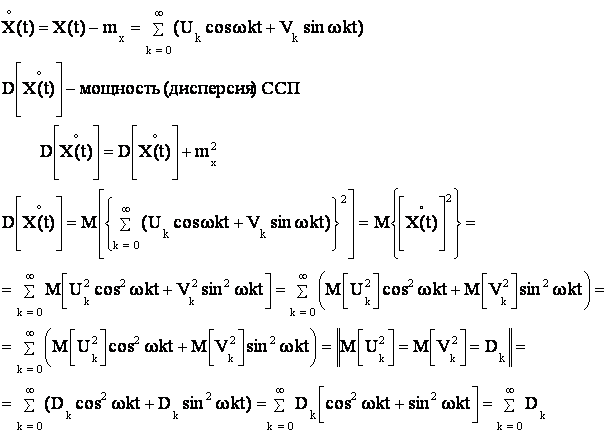     

Разложение Фурье – это разложение по амплитудам. Что бы произвести каноническое разложение X(t) достаточно знать значение ее корреляционной функции. Мощность случайного процесса распределена между гармоническими составляющими его разложения, по закону  эта зависимость называется мощностным или энергетическим спектром. Для разложения мы рассмотрим кусок процесса на интервале [0;T], а далее повторяем много раз т.о спектр получается линейчатым т.е это линейчатый энергетический спектр.