Курс лекций по дисциплине «Информационно-измерительные системы», страница 14

2.3 Корреляционная функция детерминированного сигнала.

 

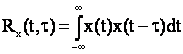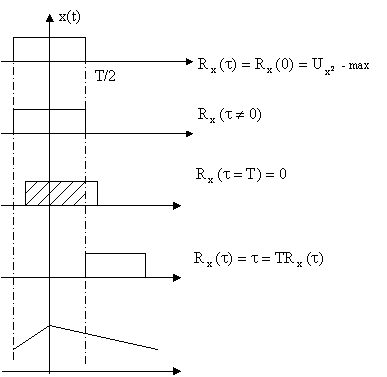Сигнал называется некоррелированным, если взаимокорреляционная функция равна нулю.

3 ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

Ранее были рассмотрены частные характеристики детерминированных сигналов. Связь между ВЧХ определяется парой преобразования Фурье.

Детерминированные сигналы не переносят информации. Информацию переносят только случайные сигналы и случайные события. Поэтому далее будем рассматривать случайные процессы (случайные функции времени). Случайный процесс не может быть описан как функция времени, т.к. его знак, форма, амплитуда являются случайными.

3.1 Усреднение усредненной характеристики процесса по ансамблю реализации

Реализация случайного процесса является случайной функцией времени, записанная на интервале 0-Т.

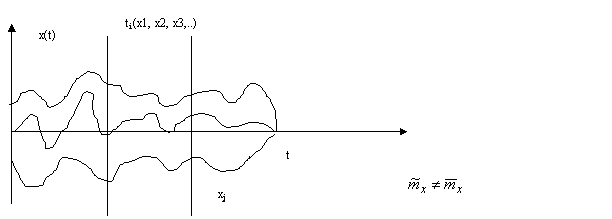
Характеристики по ансамблю реализации:

 - мощность рассеивания;

 - математическое ожидание (центр тяжести СП).

Различают стационарные () и нестационарные () случайные процессы. Для оценки СП используют точечные и интервальные характеристики.

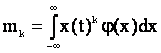
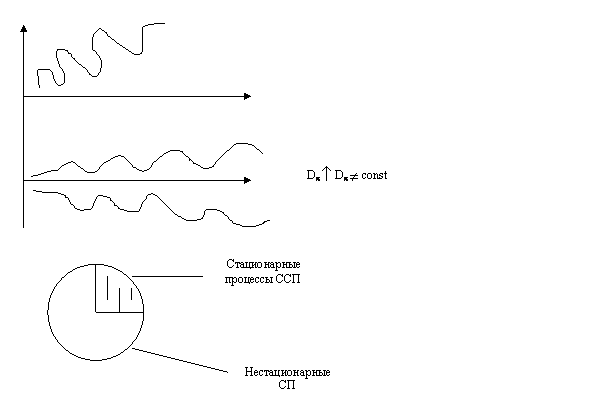
Для практического определения характеристик по ансамблю реализации, необходимо в данный момент времени произвести n – замеров случайного процесса.