Курс лекций по дисциплине «Информационно-измерительные системы», страница 21

0 1                1 1

Источник Хартли: 

;

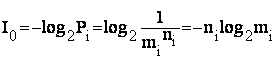
m_i – алфавит сообщения;

Пример: m_i = 32 – чиссло букв алфавита;

(бит/букву)

 – энтропия источника Хартли;

 – информационная производительность источника;

 – 1(бит/символ) – максимальная энтропия Хартли;

5.2 Источник Шеннона

Источник состоит из N – независимых символов.Символ обозначается h_i

P(h_i) = P_i – вероятность появления символа h_i.

N – общая длина характерного сообщения.

Если сообщения эргодические и достаточно длинные, то получаем:

;

;

n_i – число h_i в сообщении;

;

Т.к. вероятность появления типового сообщения длиной n – одинакова, то:

, где

N – число типовых сообщений источника Хартли.

;

;

;

;

;

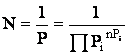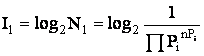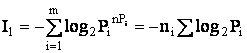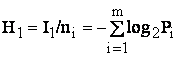При P₀ = P₁ = 1/2;     H₁=H₀ = 1 (Хартли).

1)  Граничный переход Шеннон – Хартли при P_i = const.

2)  Информативность источника Шеннона меньше информативности источника Хартли.

H₀ – энтропия источника Хартли;

m – число элементов алфавита;