Принципы исследования механизмов, страница 5

1.4 Построение плана ускорений для первого положения

Ускорение точки А

Точка А совершает вращательное движение вокруг неподвижной точки О, поэтому ее ускорение будет определятся:

Определяем масштаб ускорений

Выбираем полюс плана ускорений π и откладываем параллельно О₁А₁ , изображающий ускорение точки А в масштабе μ_а и направлена от точки А к точки О.

         Ускорение в точке В.

Точка В совершает плоско - параллельное движение.

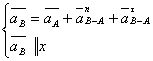 где а_в – абсолютное ускорение точки В;    - нормальное ускорение точки В при вращении ее вокруг точки А;

 - тангенциальное ускорение точки В при вращении ее вокруг точки А.

, 

аn₁ направлена от точки В к точке А и параллельно А₁В₁

 перпендикулярна А₁В₁, ему соответствует на плане ускорении n₁в. Там где n₁в пересекает линию, параллельную х, находится точка в. Πв абсолютное ускорение точки В в масштабе μ_а:

πв = 65мм 

         Ускорение точки С звена АСВ определяем на основании теоремы подобий.

 отсюда следует, что

Полученную точку С соединяем с полюсом π и получаем ускорение в точке С в масштабе.

Истинное значение ускорение точке С: πс =90мм,

         Ускорение в точке D.

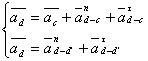
 - Кориолисово ускорение. Его величина:

,

Из полюса ускорений π откладываем отрезок πк, изображающий ускорение Кориолиса; для определения его направления вектора скорости точки D поворачиваем на 90⁰ в сторону вращения звена СЕ плана механизма.

Величина нормального ускорения точки D при вращении ее вокруг точки С определяется: ,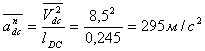 

Из тоски С на плане ускорений откладываем параллельно звену DC на плане механизма , наплавленный из точки D в точку С. Перпендикулярно звену СD на плане механизма проводим линию на плане ускорении, изображающую .

Из точки К проводим линию, перпендикулярную πк до пересечения с линией действия , в пересечении получим точку d, соединяем ее с полюсом π, получаем вектор , изображающий ускорение точки D в масштабе. Ее истинное значение:

         Ускорение в точке Е.

Соединяем точку d с точкой с на плане ускорений и продлеваем. Ускорение точки Е находим из соотношения:

 отсюда следует, что

Полученную точку e соединяем с полюсом π и получаем ускорение точки Е в масштабе.

         Ускорение в точке F.