Принципы исследования механизмов, страница 12

величины в масштабе μ_l. Величину этих отрезков в мм определяем по формуле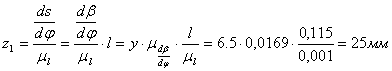 

 где  - величина первой производной линейного перемещения цен­тра ролика коромысла по углу поворота кулачка;

 - величина первой производной углового перемещения ко­ромысла по углу поворота кулачка;

l - длина коромысла;

 - масштаб длин чертежа;

 - масштаб диаграммы функции.

Длины отрезков zопределяем графически методом пропорциональ­ного деления. С этой целью определяем наибольший отрезок при уда­лении   коромысла:

Полученный отрезок откладываем на стороне произвольного pz₄ = z_max.

На второй стороне угла откладываем ординаты участка φ_у диаграммы : ру_1,7 = 1-1'; ру_2,6 = 2-2'; ру_3,5 = 3-3'; ру₄ = 4-4';

Через конечные точки отрезков ру_1,7 = 1-1'; ру_2,6 = 2-2'; ру_3,5 = 3-3' проводим прямые, парал­лельные прямой, соединяющей точки отрезка z_max и максимальной ординаты у_max, т. е. параллельно z₄y₄. Отрезки ру_1,7 = 1-1';    ру_2,6 = 2-2'и т. д. явля­ются искомыми отрезками z при удалении коромысла.

Аналогично определяем величины отрезков z при возвращении коромысла. Наибольшее значение при возвращении коромысла:

Направление вращения кулачка принимаем противоположным на­правлению вращения коромысла при его удалении. Поэтому отрезки z откладываем на промежуточных положениях коромысла вправо от ду­ги С₀ С₈ при удалении коромысла и влево — при возвращении его.

Соединив последовательно конечные точки отрезков z₁, z₂, z₃... плавной кривой, получим геометрическое место концов отрезков z[z =z (s)].

         Определяем z для остальных положений:

z₁ = z₁₆ = 25     мм; 

z₂ = z₁₅  =  50,5 мм;  

z₃ = z₁₄  =  74   мм;

z₄ = z₁₃ =  92   мм;

z₅ = z₁₂ =  74   мм;

z₆ = z₁₁ = 50,5 мм;

z₇ = z₁₀ =  25   мм; 

z₈ = z₉   =  0     мм;

Через крайние точки отрезков z проводим прямые под минимальным углом передачи γ_тin = 90 – θ = 90 – 4 = 50° к данным отрезкам. Областью центра вра­щения кулачка будет заштрихованный участок, являющийся общим для областей возможных центров вращения кулачка всех положений коромысла.

Поместим центр вращения кулачка в вершине О₂, заштрихованного участка. Длина минимального радиуса кулачка будет равна отрез­ку О₂С₀,

2.4 Профилирование кулачка.

 Профилиро­вание кулачка проводим методом обращения движения, который состоит в следующем:

         Мысленно придаем всему механизму, то есть кулачковой шайбе, коромыслу и стойке вокруг центра кулачка ω_к, которая равна, но противоположно направлена угловой скорости кулачка, тогда ω_к = 0, то есть кулачок неподвижен. Кроме перемещения и по мимо своего абсолютного движения на угол γ_тin = 90 – θ = 90 – 40 = 50° приобретая вместе со своими неподвижными параллелями добавочное движение – вращение вокруг центра О₂ кулачка с угловой скоростью, равной (-ω_к), тогда точка О его подвеса перестает оставаться  неподвижной, она описывает в обратном движении окружность R ОО₂ в направлении, прямо противоположной абсолютному вращению кулачка. Центр ролика С, помимо перемещении по дуге R ОС₀ получает добавочное движение в каждый момент времени вращение вокруг центра О₁. Но при этом его относительное расположение системе не нарушается, а следовательно метод обращение движения позволяет при проектировании рассматривать место абсолютного движения кроме его движения относительно кулачка. Сам же кулачок становится как бы неподвижным звеном. Строим треугольник ОО₂С₀ со сторонами L, l, r в масштабе μ_l = 0,001 м/мм. Радиусам равным ОС₀, проводим дугу С₀С₈, стягивающую угол С₀ОС₈ =  . Эту дугу делим на  части, пропорционально координатам диаграммы β = β(t) в сторону противоположную вращению кулачка, от линии ОО₂ откладываем углы , , ,  и проводим дугу радиуса ОО₄. Дуги, стягивающие отмеченные углы, угол подъема делим на 8 частей, а дугу  на делим на 8 частей. Из точки О проводим радиус ОС₁ дугу до пересечения с радиусам равным длине коромысла, где пересекаются получим точку 1'. Соединив плавной кривой точки, получим теоретический профиль кулачка. Затем радиусам ролика r_р = 10 мм проводим окружности, центром которых являются точки 1', 2',….24' нижняя  огибающая этих окружностей будет являться проектным профилем или рабочим.