После определения частоты автоколебаний, по показаниям датчиков ДФМ может быть найдена собственная форма, т.е. определено число узловых диаметров по окружности колеса. Следует учесть, что по вычисленной с помощью формулы (15) частоте автоколебаний (и её сопоставлению с результатами вибрационных расчётов или испытаний облопаченных дисков в Кемпбелл-машине) можно установить только, что имеют место автоколебания с узловыми диаметрами без узловых окружностей, но не конкретной число диаметров. Это связано с тем, что для лопаток последних ступеней мощных паровых турбин возрастание частот при увеличении числа узловых диаметров на единицу относительно мало и поэтому для точного их определения необходимо найти сдвиг по фазе между колебаниями различных лопаток, т.е. сравнить показания, полученные с помощью одной и той же пары датчиков для всех оснащённых магнитами лопаток.
Анализ результатов измерений свидетельствует о том, что автоколебания с различными числами узловых диаметров имеют характер «бегущей волны», т.е. максимальные прогибы разных лопаток оказываются примерно равными (с точностью до отклонений реальных облопаченных дисков от циклически-симметричных систем), но достигаются в различные моменты времени. Т.о., прогибы i-ой и j-ой лопаток – Ai(t) и Aj(t) – изменяются во времени по закону:
![]()
![]() (16)
(16)
где Ai, Aj – амплитуды соответственно i-ой и j-ой лопаток, Djij – угловое расстояние между i-ой и j-ой лопатками, m – число узловых диаметров, а знак перед последним слагаемым во второй из формул (16) определяется тем, совпадает ли направление распространения «бегущей волны» с направлением вращения ротора или ему противоположно. С учётом сказанного выше о неизбежных технологических отклонениях облопаченного диска от идеальной циклически-симметричной системы, будем в общем случае считать величины Ai и Aj несколько отличными друг от друга.
Измерение колебаний i-ой и j-ой лопаток происходит в дискретные моменты времени, определяемые формулой:
tik = ti0 +(2p/w)k, tjk = ti0 +(2p/w)k +(Djij/w), (17)
где, как и ранее, целое число k определяет номер замера, а положительный знак последнего слагаемого во второй формуле (17) означает, что j-ая лопатка проходит мимо пары индукционных датчиков позднее i-ой.
Связь между изменением показаний датчиков при k-ом замере и отклонениями i-ой и j-ой лопаток с учётом формулы (16) запишем в следующем виде:
DSik = Ai kпi cos ptik, DSjk = Aj kпj cos [ptik ±Djijm +(Djijp/w)], (18)
где коэффициенты kпi и kпj учитывают небольшие различия в местах установки магнитов и навалах лопаток.
Повторив выкладки, аналогичные выполненным ранее, можно получить следующее приближённое выражение:
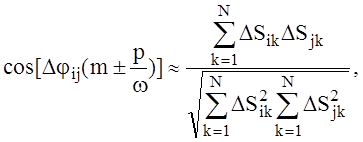 (19)
(19)
где, как и ранее, N – общее число замеров, причём точность приближённого равенства (19) возрастает по мере увеличения N. Величина (p/w)±m в левой части формулы (19) заменена на m±(p/w) с учётом того, что, как правило, m>(p/w), а функция cos является чётной.
Вычислив правую часть формулы (19) для всех пар соседних оснащённых магнитами лопаток, найдя величины Djij[m±(p/w)] и просуммировав их, можно формально, с учётом знака в левой части формулы, найти два значения числа узловых диаметров m. При определении числа диаметров следует учитывать, что имеет место равенство:
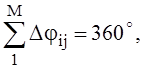 (20)
(20)
где М – число оснащённых магнитами лопаток на диске.
«Правильный» знак в левой части формулы (19) должен дать целое значение числа m (с малыми отклонениями, вызванными погрешностями измерений и вычислений). Единственная трудность может возникнуть в том случае, когда величина p/w окажется близкой к целому числу с половиной, а тогда, в соответствии с формулой (19), может быть найдено два «почти целых» числа узловых диаметров m. Истинное значение m в этом случае следует выбрать с учётом найденной экспериментально частоты автоколебаний p, а также результатов расчётов и экспериментов, выполненных при тензометрических вибрационных испытаниях вращающихся облопаченных дисков на заводских стендах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.