Автоколебания рабочих лопаток паровых турбин (измерения, анализ, меры борьбы). Учебное пособие, страница 23

                    R₁ ~ Fu / f ~ Fs / f E,                                                                           (53)

где s - максимальные динамические напряжения в лопатке при резонансе, Е – модуль упругости 1 рода. Справедливость последнего соотношения в формуле (53) определяется тем, что между величиной максимальных напряжений и скоростью колебаний периферийного сечения для большинства имеющих практическое значение собственных форм существует универсальная связь  (s~u E), слабо зависящая от геометрических характеристик лопаток [5].

          Рассеянная за цикл энергия R₂ пропорциональна потенциальной энергии системы и декременту колебаний d [5]. Т.к. потенциальная энергия пропорциональна  Vs² (где  V – объём профильной части лопатки), то величину  

R₂ можно представить в виде:

                    R₂ ~ d s² V ~ d u² E² V.                                                            (54)

          Приравняв подведённую и рассеянную за цикл энергии, получим известную зависимость между уровнем напряжений при резонансе, амплитудой возмущающей силы и величиной декремента:

                    s ~ F/d.                                                                                      (55)

          Из выражения (55) следует, что уровень напряжений при резонансе прямо пропорционален амплитуде возмущающей силы и обратно пропорционален декременту колебаний. При постепенном возрастании возмущающих сил, например, при увеличении мощности турбины, будет происходить и постепенное возрастание уровня напряжений в лопатках (практически рост напряжений будет происходить несколько медленнее, т.к. величина декремента, как правило, также увеличивается при возрастании напряжений).

          Принципиально другой при сделанных предположениях будет закономерность, определяющая амплитуду автоколебаний. Как было показано выше, сила, вызывающая автоколебания, пропорциональна скорости колебаний (уровню динамических напряжений в лопатках). Т.о., в данном случае и подведённая, и рассеянная энергия будут пропорциональны квадрату скорости колебаний.

          Например, при использовании приближённой формулы (50) и условии независимости декремента от уровня напряжений, можно записать:

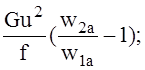                     ~       R₂ ~ d u² E² V.                                    (56)

          Если выполняется условие:

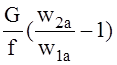                    < С d,                                                                     (57)

где С – коэффициент, зависящий от геометрических характеристик и материала лопатки, формы колебаний и параметров потока, то автоколебания вообще не возникнут, а если по какой-либо причине лопатки отклонятся от положения равновесия, то колебания будут затухающими.

          Если же, наоборот, будет выполняться условие:

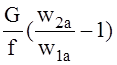                    > С d,                                                                     (58)

то амплитуда автоколебаний при сделанных упрощающих предположениях будет неограниченно возрастать.

          Естественно, что в подавляющем большинстве случаев как при колебаниях отдельных лопаток, так и лопаток, соединённых упруго-фрикционными связями, декремент возрастает    по мере увеличения амплитуды, т.е. в определённом интервале изменения скоростей колебаний или динамических напряжений приближённо может быть представлен в виде:

          d(u) = d₀ + a₁u      или      d(s) = d₀ + a₂s.                                          (59)

          При выполнении условия (59) можно записать следующее выражение для энергии, рассеянной за цикл колебаний:

                    R₂ = b₁d₀u² + b₂u³,                                                                              (60)

где b₁ и  b₂ – коэффициенты, зависящие от геометрических характеристик лопаток и связей, формы колебаний, свойств материала, особенностей работы контактного соединения, технологии и качества сборки и т.д.

Используя формулу (56), представим выражение для подведённой за цикл энергии в следующем виде: