т.е. переменное усилие будет действовать в направлении, противоположном скорости, и поэтому не только не способствует возникновению автоколебаний, но даже обеспечивает дополнительное рассеяние энергии (вызывает аэродемпфирование). Когда через половину периода скорость колебаний лопатки поменяет знак, то одновременно изменится и знак переменного усилия, которое по-прежнему будет находиться в противофазе со скоростью колебаний. Принципиально другой характер носит силовое взаимодействие лопатки с потоком при возникновении аксиальной скорости колебаний (рис.18б).
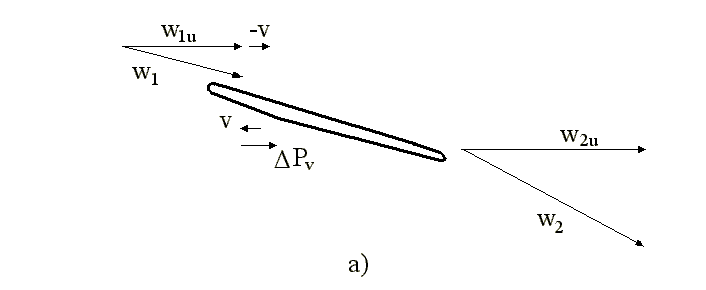
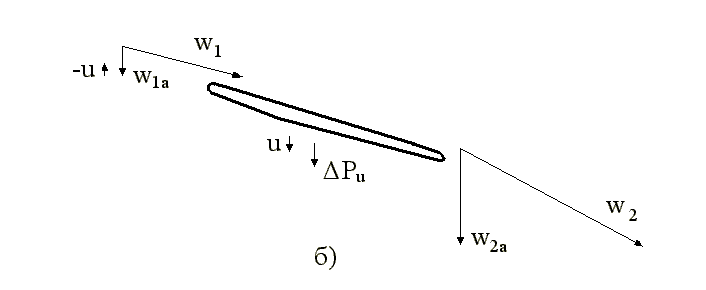
Рис.18. Изменение скоростей и усилий при возникновении тангенциальной (а) и аксиальной (б) скорости колебаний лопатки.
Известно, что величина осевого усилия, действующего на элемент лопатки единичной высоты при отсутствии колебаний, определяется формулой [6]:
Pa = (p1-p2) t - G(w2a – w1a), (47)
где p1, p2, w1a, w2a - величины давлений и осевых скоростей соответственно на входе и выходе из решётки рабочих лопаток, t – шаг в рассматриваемом поперечном сечении.
Учитывая сделанное ранее упрощающее предположение о квазистационарном характере взаимодействия лопатки с потоком, точных количественных результатов, естественно, получить не удастся. Для получения качественных соотношений между переменными осевыми силами и скоростями введём дополнительное предположение о том, что после возникновения автоколебаний величины p1 и p2 сохраняются неизменными. Основанием для такого предположения является то, что после возникновения дисковых колебаний суммарное аэродинамическое сопротивление решётки рабочих лопаток сохраняется неизменным, а осевые зазоры между направляющими и рабочими лопатками в последних ступенях весьма велики. При сделанных упрощениях после возникновения осевой скорости лопатки (u) величина действующего на неё переменного усилия (DPa) будет определяться только изменением второго слагаемого в формуле (47). Как и ранее, рассмотрим взаимодействие потока с лопаткой в момент, когда скорость колебаний достигнет максимального значения (для определённости будем считать, что лопатка проходит положение равновесия и с максимальной осевой скоростью движется в сторону выхлопного патрубка – рис.18б). В этом случае для величины DPa можно записать следующее соотношение:
DPa =-G¢(w2a¢-w1a¢) + G (w2a-w1a), (48)
где значком ¢, как и ранее, отмечены параметры потока после возникновения колебаний.
При сделанных упрощающих предположениях справедливы соотношения:
w1a¢ = w1a -u; G¢ = G (w1a - u)/w1a, (49)
кроме того, можно приближённо считать, что (w2a¢/w1a¢)»(w2a/w1a), поскольку при p1=const, p2=const перепад на рабочую решётку и плотность потока до и за рабочими лопатками сохраняются неизменными.
С учётом этих соотношений формулу (48) можно преобразовать к виду:
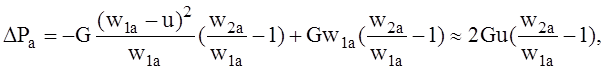 (50)
(50)
причём при выводе формулы пренебрегалось малыми величинами типа u2.
Т.к. в последних ступенях мощных паровых турбин отношение w2a/w1a значительно больше единицы, то из формулы (50) следует, что при возникновении аксиальной скорости колебаний появляется сила, находящаяся в фазе со скоростью, т.е. способная привести к возникновению автоколебаний. Физический смысл появления подобной силы состоит в том, что при рассматриваемом движении лопатки в сторону выхлопного патрубка уменьшается количество пара, поступающего в канал и получающего ускорение в аксиальном направлении. При уменьшении расхода пара уменьшается и величина силы, действующей от лопатки на поток в сторону патрубка. Т.к. сила, действующая от потока на лопатку, равна по величине, но противоположна по знаку, то при движении лопатки в сторону патрубка уменьшается сила, направленная против движения, т.е. дополнительно к постоянной силе, имеющей место при отсутствии колебаний, возникает переменное усилие, пропорциональное скорости колебаний и совпадающее с ней по направлению. Через половину периода колебаний меняет знак как направление скорости, так и направление силы, т.е. также сохраняется подвод энергии от потока к колеблющейся лопатке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.