Автоколебания рабочих лопаток паровых турбин (измерения, анализ, меры борьбы). Учебное пособие, страница 13

          На основании вычислений, аналогичных выполненным выше, получим: A^°=3669,08^°; m=10,192 ± 2,825 или m₁=7,367; m₂=13,017, т.е. истинное число узловых диаметров m=13. Т.о., в соответствии с данными таблиц №2 и №3 получим, что увеличению частоты автоколебаний со 133 до 141,3 Гц  соответствует увеличение числа узловых диаметров с 9 до 13.

          Использование формулы (19), как отмечалось в предыдущем разделе, соответствует предположению, что автоколебания носят характер «бегущей волны». Это означает, что, хотя в определённый момент времени амплитуды лопаток по окружности колеса изменяются по закону cos mj, однако узловые диаметры не привязаны к конкретным точкам диска, а перемещаются со временем в окружном направлении. По этой причине амплитуды всех лопаток оказываются равными друг другу, но достигаются в разные моменты времени. Естественно, что равенство амплитуд выполняется лишь приближённо, поскольку по технологическим причинам реальные облопаченные диски неизбежно имеют отклонения от циклически-симметричных систем. О близости амплитуд различных лопаток при автоколебаниях, имевших место при нагрузках N=0,6N_ном. и N=0,75N_ном., свидетельствуют данные, приведённые на рис.13. При построении графиков относительные амплитуды различных лопаток (А_отнi) вычислялись по формуле:

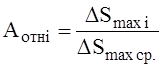                                                                                           (42)