f = q n ± fизм , (6)
где f = p/2p, n – число оборотов ротора в секунду.
Связь между истинным и «измеренным» процессом иллюстрируется рис.2, где приведено сравнение синусоидального процесса с частотой 122 Гц и его регистрация датчиками ДФМ (случай, имевший место на практике).
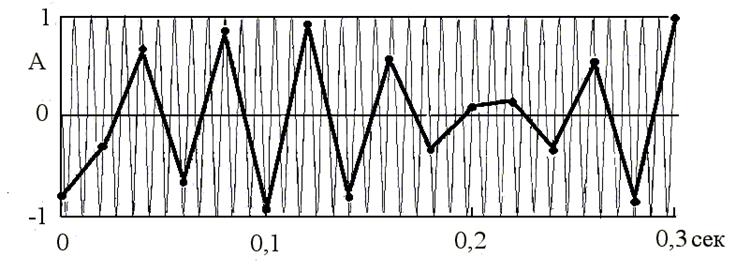
Рис.2. Сравнение истинного и «измеренного» с помощью датчиков ДФМ процесса колебаний при малой частоте опроса.
Рассмотрим, как нужно изменить методику измерений, чтобы надёжно определить не только амплитуду, но и частоту автоколебаний, поскольку только знание частоты даёт возможность связать амплитуду с уровнем динамических напряжений в лопатках [3].
Т.к. за время, соответствующее одному обороту ротора, лопатка гарантированно совершит более, чем одно целое колебание, то необходимо произвести дополнительное измерение через более короткий промежуток времени, т.е. выполнить замер в другой точке окружности с помощью второй пары датчиков ДФМ.
Если угловое расстояние между двумя парами датчиков ДФМ равняется Dj, то, в соответствии с формулой (4), фаза колебаний лопатки за время прохождения ею расстояния между первой и второй парами датчиков изменится на величину:
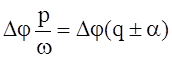(7)
По результатам измерений можно вычислить сумму:
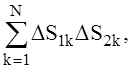(8)
где DS1k, DS2k - отклонения от соответствующих средних значений для первой и второй пар датчиков при k-ом замере, т.е. в момент времени t=tk для первой пары и t=tk+(Dj/w) для второй, N – общее число замеров.
Используя выражения (2) и (3) и учитывая, что входящий в формулу (2) коэффициент пропорциональности kп может немного отличаться для первой и второй пар (например, из-за небольшого различия в углах установки сердечников датчиков b, величинах радиальных зазоров и осевых смещений), выражения DS1k, DS2k и сумму (8) перепишем в следующем виде:
DS1k = A kп1 sin ptk,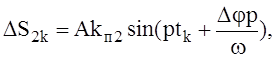 
(9)
.
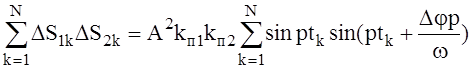(10)
Используя свойства тригонометрических функций, найдём:
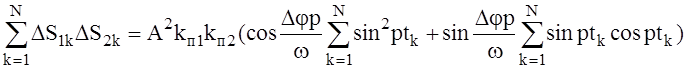(11)
Т.к. частоты p и w не кратны друг другу, то фазовый угол ptk при произвольном k-ом замере может с равной вероятностью принять любое значение в интервале от 0 до 2p. При этом условии и наличии достаточно большого числа точек замеров N можно записать приближённые равенства:
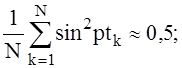
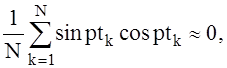(12)
поскольку справедливы формулы:
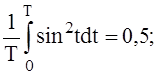
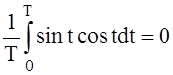при Т®¥.
С учётом формул (12) преобразуем равенство (11) к виду:
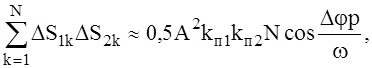(13)
тем более точное, чем больше число слагаемых N.
Помимо суммы (8), вычислим также суммы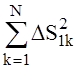 
и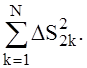 
Повторяя преобразования, аналогичные выполненным ранее, найдём:
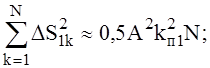
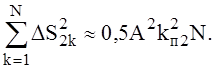(14)
Используя выражения (13) и (14), окончательно получим:
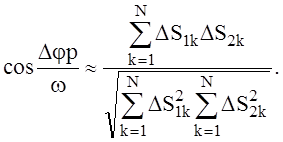(15)
Вычислив суммы, входящие в правую часть равенства (15), можно найти величину cos (Djp/w), а затем, зная угловое расстояние между парами датчиков Dj, определить круговую частоту колебаний p и частоту колебаний f. Учитывая неоднозначность тригонометрических функций, должно выполняться неравенство 0<(Djp/w)<p, т.е. величина Dj должна быть тем меньше, чем больше ожидаемое отношение p/w.
Точность приближённой формулы (15) оказывается тем выше, чем больше число слагаемых N. В [3] приведены результаты расчётов, свидетельствующие о том, что уже при N=50-100 (т.е. при выполнении измерений в течение 1-2 секунд) погрешность при определении частоты не превышает нескольких %. При измерениях в течение нескольких десятков секунд формулы (12) и, следовательно, (15) можно считать практически точными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.