































Глава 2
Устойчивость линейных систем
2.1. Определение и условия устойчивости
линейных систем
Определение: линейная система называется устойчивой, если при отсутствии воздействия (g(t)=0) и любом начальном условии Y(t0) состояние системы Y(t) стремится к нулю при t→∞.
Из данного определения следует, что устойчивость – это свойство самой линейной системы, не зависящее от g(t). Кроме того, устойчивость линейной системы – бинарный показатель качества, принимающий одно из 2-х значений: система устойчива или система неустойчива.
Рассмотрим однородное дифференциальное уравнение линейной системы 1-го порядка:
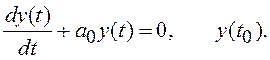 (2.1)
(2.1)
Решение (2.1) имеет вид:
![]()
При a0>0 система, описываемая уравнением (2.1), устойчива, так как y(t) стремится к нулю при t→∞. Это условие устойчивости системы 1-го порядка.
Рассмотрим однородное дифференциальное уравнение системы n-го порядка:
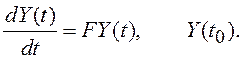 (2.2)
(2.2)
Анализ условий
устойчивости системы, описываемой уравнением (2.2), при произвольной матрице F
затруднен из-за наличия перекрестных связей. Например, при n=2 и 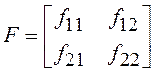 (fij – произвольные вещественные числа; i,j =1,2) система содержит два интегратора, состояние
которых характеризуется переменными y1 и y2. Один из
интеграторов (с состоянием y1) охвачен
обратной связью с коэффициентом f11, а другой (с состоянием y2) – с коэффициентом f22. Коэффициенты
f12 и f21 определяют перекрестные связи:
коэффициент f12 учитывает влияние y2 на dy1/dt,
а коэффициент f21 – влияние y1 на dy2/dt.
Если матрица F имеет диагональную форму, перекрестные связи отсутствуют
и анализ устойчивости системы упрощается.
(fij – произвольные вещественные числа; i,j =1,2) система содержит два интегратора, состояние
которых характеризуется переменными y1 и y2. Один из
интеграторов (с состоянием y1) охвачен
обратной связью с коэффициентом f11, а другой (с состоянием y2) – с коэффициентом f22. Коэффициенты
f12 и f21 определяют перекрестные связи:
коэффициент f12 учитывает влияние y2 на dy1/dt,
а коэффициент f21 – влияние y1 на dy2/dt.
Если матрица F имеет диагональную форму, перекрестные связи отсутствуют
и анализ устойчивости системы упрощается.
Используем линейное преобразование Y(t)=ΛY0(t) с неособенной матрицей Λ. Тогда из (2.2) получаем
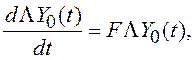 откуда
откуда
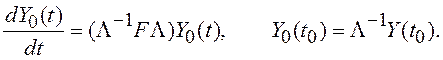 (2.3)
(2.3)
Решение уравнения (2.3) при t0=0 имеет вид:
![]()
Анализ условий устойчивости системы, описываемой уравнением (2.3), оказывается весьма простым при диагональной форме матрицы
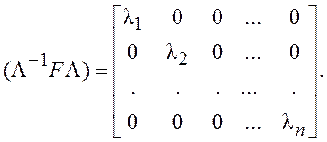
Числа λ1, λ2, …, λn (в общем случае – комплексные) называются собственными значениями матрицы F. Подстановка любого из этих чисел (λ=λi, i=1,2,…,n) в матрицу (λI-F) превращает ее в вырожденную матрицу с нулевым определителем:
![]() (2.4)
(2.4)
Левая часть (2.4) называется характеристическим многочленом матрицы F (матрицы F и (Λ-1FΛ) подобны и имеют один и тот же характеристический многочлен), а само уравнение (2.4) называется характеристическим уравнением системы, описываемой уравнением (2.2).
Таким образом, собственные значения матрицы F – λ1, λ2, …, λn – определяются в результате решения характеристического уравнения (2.4).
В случае диагональной формы матрицы (Λ-1FΛ) соответствующая ей переходная матрица также имеет диагональную форму:
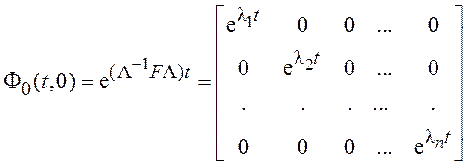 .
.
(В этом нетрудно убедиться, разложив матричную экспоненту в ряд в соответствии с рекомендациями разд.1.12).
В результате диагонализации матрицы (Λ-1FΛ) в системе, описываемой уравнением (2.3), перекрестные связи отсутствуют. Это означает, что n-мерная система (2.2) распалась на n 1-мерных систем (выполнена декомпозиция системы):
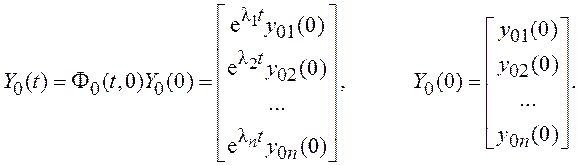 (2.5)
(2.5)
Возвращаемся к вектору состояния Y(t) исходной системы, описываемой уравнением (2.2):
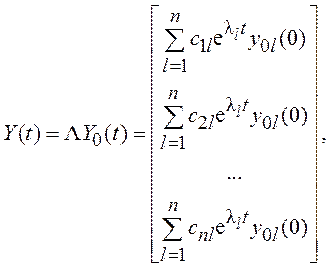 (2.6)
(2.6)
где ckl – элементы матрицы Λ; k=1,2,…,n.
В устойчивой системе все экспоненты в правой части (2.6) должны стремиться к нулю при t→∞, а поведение экспонент зависит от собственных значений матрицы F. Если все λ1, λ2, …, λn вещественны, то условие устойчивости записывается в виде: λi<0, i=1,2,…,n. Если среди собственных значений λ1, λ2, …, λn имеются комплексно-сопряженные λi=αi+jβi и λi+1=αi-jβi (рассматриваем случай, когда характеристическое уравнение имеет вещественные коэффициенты), то их сумма в (2.6) описывает колебательный процесс:
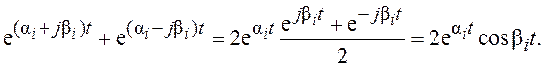
Этот процесс затухает при t→∞, если αi<0.
Следует заметить, что матрица F приводится к диагональной матрице (Λ-1FΛ) лишь в случае, когда все собственные значения матрицы F различны. Если имеются кратные собственные значения, то матрица F приводится к канонической жордановой форме с собственными значениями на главной диагонали:
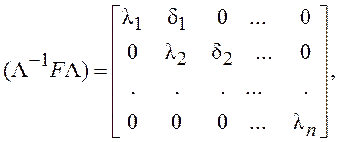
причем δi=1, если λi= λi+1 и δi=0 в
остальных случаях. Диагональный блок с одинаковыми собственными значениями
называется жордановой клеткой. При этом выполняется частичная декомпозиция
системы с сохранением некоторых (односторонних) связей. Для собственного
значения λi
кратности k жордановой клетке 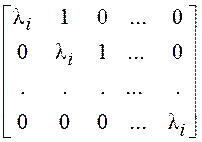 сопоставляется переходная матрица вида
сопоставляется переходная матрица вида
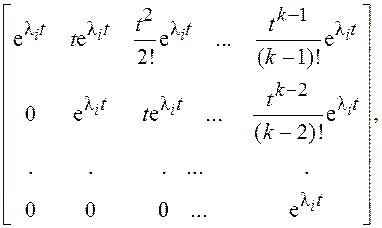
поэтому строки с индексами i, i+1,…,i+k-1
в выражении (2.5) заменяются суммами: 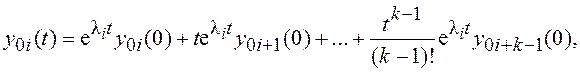
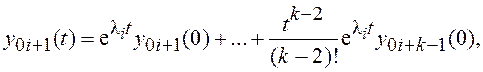
…………………..
![]()
Все слагаемые этих сумм при t→∞ также затухают, если λi имеет отрицательную вещественную часть.
Таким образом, условие устойчивости линейной непрерывной системы, представленной в пространстве состояний, формулируется следующим образом: для обеспечения устойчивости системы необходимо и достаточно, чтобы все собственные значения матрицы F имели отрицательные вещественные части.
Установим связь между собственными значениями матрицы F и полюсами ПФ замкнутой системы. Для этого воспользуемся полученным в разд. 1.12 выражением (1.41):
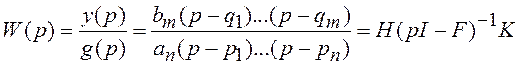
(нули q1,…,qmи полюсы p1,…,pn ПФ определены в разд. 1.2).
Известно правило вычисления обратной матрицы:
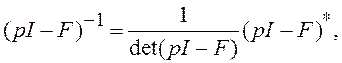
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.