Устойчивость линейных систем. Критерий Рауса-Гурвица. Коррекция с помощью местной обратной связи, страница 4

При ω=0 кривая Михайлова начинается на положительной части вещественной оси, если K>0. С учетом необходимого условия устойчивости должны также выполняться неравенства: T>0 и τ>0. Рассматриваемая система имеет порядок n=3, следовательно, кривая Михайлова должна пересечь положительную часть мнимой оси и отрицательную часть вещественной оси. В точке пересечения мнимой оси выполняется условие K-ω²=0, откуда  (ω₁ – частота, соответствующая точке пересечения мнимой оси кривой Михайлова). Для обеспечения устойчивости требуется выполнение условия:  откуда при  имеем τ>T. Таким образом, ограничения на параметры устойчивой системы следующие: K>0, T>0, и τ>T. На рис. 2.2 показаны кривые Михайлова устойчивой (кривая 1) и неустойчивой (кривая 2) систем.

4. Критерий Найквиста.

          Этот критерий предложен американским ученым Г. Найквистом в 1932 г. для исследования усилителей с отрицательной обратной связью. В дальнейшем, этот критерий был применен А.В. Михайловым в теории автоматического регулирования для анализа устойчивости статических и астатических систем управления. В отличие от рассмотренных ранее критериев, здесь анализ устойчивости замкнутой системы сводится к анализу свойств системы в разомкнутом состоянии. Используется ПФ разомкнутой системы с заменой p на jω, т.е. частотная характеристика W_р(jω). Годограф частотной характеристики W_р(jω) называют годографом Найквиста (см. разд. 1.3).

          Интересующие нас устройства радиоавтоматики в подавляющем большинстве представляют собой одноконтурные системы, в которых отсутствуют местные обратные связи (если местные обратные связи в системе присутствуют, то, как правило, соединения с включением звена в цепи обратной связи можно представить в виде апериодического или колебательного звеньев). Дадим формулировку критерия Найквиста для случая одноконтурных систем: для обеспечения устойчивости системы необходимо и достаточно, чтобы годограф Найквиста не охватывал точку на комплексной плоскости с координатами (-1, j0). При этом, для получения замкнутой кривой, годограф Найквиста статических систем 1 дополняется вещественной положительной полуосью, а для астатических – еще и дугой окружности бесконечного радиуса, соединяющей начало годографа 2 (ω=0) с вещественной положительной полуосью против часовой стрелки (рис. 2.3).

Точка пересечения годографа Найквиста и единичной окружности соответствует частоте среза системы ω_ср (‌‌‌). Точка пересечения годографа Найквиста и вещественной отрицательной полуоси  соответствует критической частоте системы ω_кр (φ(ω_кр)=-180^о). Эти точки показаны на рис. 2.3 для астатической системы (кривая 2).

          Система находится на границе устойчивости, если годограф Найквиста проходит через точку (-1, j0). Удаление системы от границы устойчивости характеризуют

- запас устойчивости по фазе  (определен в разд. 1.5),

- запас устойчивости по амплитуде 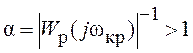 (используется только для абсолютно устойчивых систем, которые теряют устойчивость лишь при увеличении коэффициента усиления).

2.3. Минимально-фазовые системы

          Частным случаем устойчивых систем являются минимально-фазовые системы, для которых выполняется следующее условие: нули и полюсы ПФ минимально-фазовой системы имеют отрицательные вещественные части.

          Отметим некоторые свойства минимально-фазовых систем.

1. Минимально-фазовые системы устойчивы.

2. При инвертировании ПФ минимально-фазовой системы получается ПФ также минимально-фазовой системы.

3. Для минимально-фазовой системы с частотной ПФ W(jω) существует однозначная связь между вещественной P(ω) и мнимой Q(ω) частотными характеристиками, а также между амплитудной  и фазовой φ(ω) частотными характеристиками. Эта связь определяется известным преобразованием Гильберта.

          Таким образом, зная какую-либо одну частотную характеристику минимально-фазовой системы, можно однозначно определить все другие частотные характеристики.

          Класс минимально-фазовых систем довольно обширен. В частности, он включает в себя рассмотренные в разд. 1.4 типовые элементарные звенья с положительными параметрами (кроме интегрирующего и дифференцирующего звеньев, которые следует рассматривать как исключение). Однозначная связь между  и φ(ω) для минимально-фазовых систем наглядно проявляется при построении логарифмических характеристик.