Устойчивость линейных систем. Критерий Рауса-Гурвица. Коррекция с помощью местной обратной связи, страница 2

где  - присоединенная матрица, составленная из алгебраических дополнений.

          Следовательно, знаменатель ПФ замкнутой системы с точностью до постоянного множителя совпадает левой частью характеристического уравнения (2.4), а полюсы ПФ замкнутой системы и собственные значения матрицы F равны: λ_i=p_i, i=1,2,…,n. При этом условие устойчивости линейной непрерывной системы, описанной с помощью ПФ, формулируется следующим образом: для обеспечения устойчивости системы необходимо и достаточно, чтобы все полюсы ПФ замкнутой системы имели отрицательные вещественные части.

          В качестве примера, иллюстрирующего использование условий устойчивости, рассмотрим задачу анализа устойчивости СУ, структурная схема которой показана на рис. 2.1.

          В случае описания системы в ПС матрица F равна 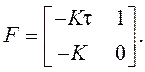 Вычисляем  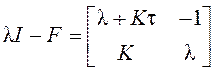и записываем характеристическое уравнение:

          Собственные значения матрицы F являются корнями этого уравнения:

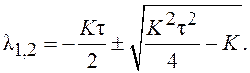                                                    (2.7)

          Вещественная часть корней будет отрицательной, если Kτ>0 (первое слагаемое в (2.7) отрицательно) и K>0 (второе слагаемое в (2.7) меньше первого). Совместное решение этих неравенств приводит к следующим ограничениям на параметры устойчивой СУ: K>0, τ>0.

          В случае описания системы с помощью ПФ имеем:

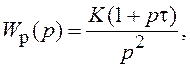  откуда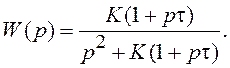  

Приравниваем знаменатель ПФ замкнутой системы W(p) к нулю и получаем то же самое характеристическое уравнение.

          В зависимости от выбранных параметров K и τ полюсы ПФ (собственные значения матрицы F) могут быть вещественными и комплексно-сопряженными. Кратные вещественные полюсы разделяют эти множества. Из условия 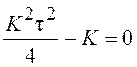 можно найти дополнительное ограничение на параметры устойчивой СУ, ПФ которой имеет кратные вещественные полюсы: 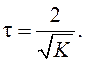 Нетрудно вычислить переходную матрицу и убедиться, что при t₀=0 и 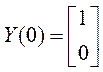 решение однородного дифференциального уравнения системы в этом случае имеет вид процесса, близкого к монотонному:

          Заметим, что распределение корней характеристического уравнения на плоскости комплексной переменной характеризует качество переходного процесса устойчивой системы (это сравнительная оценка). Удаление корней от мнимой оси определяет степень затухания переходного процесса (чем дальше корни от мнимой оси, тем меньше время нарастания переходного процесса). Отношение наибольшего коэффициента мнимой части корня к вещественной его части определяет степень колебательности переходного процесса (чем больше это отношение, тем выше степень колебательности).

2.2. Критерии устойчивости линейных

непрерывных систем

Рассмотренные в разд. 2.1 условия устойчивости СУ требуют решения характеристического уравнения:

                             (2.8)

          Существуют косвенные методы проверки устойчивости, не требующие решения характеристического уравнения. Такие методы называют критериями устойчивости. Отсутствие необходимости решения характеристического уравнения – не единственное достоинство критериев устойчивости. Для обеспечения устойчивости необходимо должным образом манипулировать параметрами СУ, а связь между корнями характеристического уравнения и параметрами СУ не всегда очевидна (см. пример разд. 2.1). Поэтому применение критериев устойчивости часто оказывается удобнее.

          1. Необходимое условие устойчивости.

          Нетрудно убедиться, что для устойчивой системы все коэффициенты характеристического уравнения (2.8) строго положительны: a_i>0, i=0,1,…,n. Чтобы показать это, представим левую часть (2.8) в виде:

                                    (2.9)

Если p_i – вещественный корень: p_i=-α_i, α_i>0, то соответствующий сомножитель в (2.9) имеет вид: p+α_i и представляет собой многочлен (двучлен) с положительными коэффициентами. Если p_i и p_i+1 – комплексно-сопряженные корни: p_i=-α_i+jβ_i и p_i+1=-α_i-jβ_i, α_i>0, β_i>0, то соответствующие сомножители в (2.9) имеют вид:  и представляют собой многочлен (трехчлен) с положительными коэффициентами. Следовательно, левая часть характеристического уравнения является произведением многочленов с положительными коэффициентами, поэтому a_i>0, i=0,1,…,n.