С целью выявления
особенностей не минимально-фазовых систем рассмотрим звено с ПФ 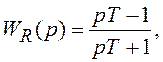 имеющей положительный нуль.
Амплитудно-фазовая характеристика этого звена показана на рис. 2.4, а. Нетрудно
определить амплитудно-частотную
имеющей положительный нуль.
Амплитудно-фазовая характеристика этого звена показана на рис. 2.4, а. Нетрудно
определить амплитудно-частотную ![]() и фазочастотную
и фазочастотную 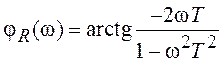 характеристики звена.
характеристики звена.
Выражение для ![]() , с учетом известных тригонометрических
соотношений, можно записать в виде:
, с учетом известных тригонометрических
соотношений, можно записать в виде: ![]()
Теперь становится понятным
термин – минимально-фазовая система. Это такая система, которая для любой
частоты ω имеет наименьший сдвиг фазы φ(ω) по сравнению с другими системами,
обладающими такой же амплитудно-частотной характеристикой. В данном примере
минимально-фазовым является усилительное звено с ПФ ![]() и фазочастотной характеристикой φ(ω)=0.
и фазочастотной характеристикой φ(ω)=0.
Поскольку ![]() то ЛАХ звена с ПФ
то ЛАХ звена с ПФ ![]() совпадает с ЛАХ форсирующего звена, а ЛФХ имеет вид:
совпадает с ЛАХ форсирующего звена, а ЛФХ имеет вид: ![]() Сдвиг фазы у звена с ПФ
Сдвиг фазы у звена с ПФ ![]() оказывается больше, чем у минимально-фазового форсирующего
звена. Кроме того, нарушена привычная для минимально-фазовых систем связь ЛАХ и
ЛФХ.
оказывается больше, чем у минимально-фазового форсирующего
звена. Кроме того, нарушена привычная для минимально-фазовых систем связь ЛАХ и
ЛФХ.
Заметим, что звенья, подобные звену с
ПФ ![]() у которых только ЛФХ зависит от
частоты, иногда применяются для коррекции систем. При реализации звена с ПФ
у которых только ЛФХ зависит от
частоты, иногда применяются для коррекции систем. При реализации звена с ПФ ![]() можно, например, использовать следующее преобразование ПФ
апериодического звена
можно, например, использовать следующее преобразование ПФ
апериодического звена ![]()
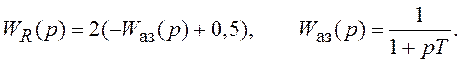
На рис. 2.4, б показана трансформация АФХ апериодического звена при выполнении указанных преобразований.
2.4. Коррекция систем управления
Под коррекцией будем понимать включение в состав СУ дополнительных (корректирующих) элементов с целью улучшения ее показателей качества. Заметим, что задача обеспечения требуемых точностных характеристик СУ обычно не входит в круг решаемых при коррекции задач (эта задача решается другими средствами, освещаемыми в разд. 3). Поэтому целью коррекции, как правило, может быть:
- обеспечение устойчивости,
-улучшение качества переходного процесса (снижение степени колебательности, величины перерегулирования и времени нарастания переходного процесса),
- достижение лучшей помехоустойчивости.
В зависимости от способа включения корректирующих элементов различают следующие методы коррекции:
- последовательный метод коррекции,
- параллельный метод коррекции,
- метод коррекции с включением звена в цепи обратной связи.
Все методы коррекции с точки зрения достижения полезного эффекта эквивалентны. Поэтому при выборе метода коррекции следует учитывать простоту реализации корректирующих элементов и некоторые дополнительные факторы (влияние нелинейностей, нестабильность параметров и т.п.). Следует также учесть, что последовательный метод коррекции для большинства устройств радиоавтоматики наиболее прост в реализации.
1. Последовательный метод коррекции.
Корректирующий элемент с ПФ Wк(p) включается последовательно в исходную СУ с ПФ Wи(p). Поскольку результирующая (желаемая) ПФ равна Wж(p)= Wи(p) Wк(p), нетрудно, при известных Wи(p) и Wж(p), найти
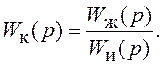 (2.12)
(2.12)
Обычно коррекция выполняется с построением ЛХ. Для ЛАХ соотношению (2.12) соответствует:
![]() (2.13)
(2.13)
Условие (2.13) дополняется двумя ограничениями:
1) низкочастотные асимптоты Lи(ω) и Lж(ω) должны совпадать (коррекция не должна оказывать влияние на точностные характеристики СУ, поэтому коэффициент усиления системы и ее порядок астатизма при коррекции, как правило, не изменяют);
2) корректирующий элемент должен быть физически реализуем (порядок многочлена числителя ПФ Wк(p) не должен превышать порядка многочлена знаменателя).
Для выполнения 2-го ограничения рекомендуется не просто задавать ПФ Wж(p), а использовать типовые (заведомо реализуемые) корректирующие элементы с известными ПФ Wтк(p). Рассмотрим некоторые из них.
1) Пропорционально-дифференцирующее звено с ПФ
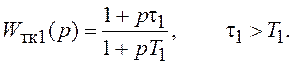
На рис. 2.5 (графики 1)
показаны ЛХ этого звена. ПФ Wтк1(p) может быть реализована с помощью схемы, показанной
на рис. 2.6, а. В этом случае 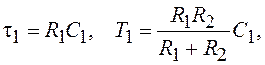 а ослабление по постоянному току,
равное
а ослабление по постоянному току,
равное 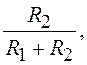 компенсируется усилителем, имеющим
коэффициент усиления
компенсируется усилителем, имеющим
коэффициент усиления 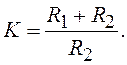
2) Пропорционально-интегрирующее звено с ПФ
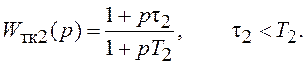
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.