Устойчивость линейных систем. Критерий Рауса-Гурвица. Коррекция с помощью местной обратной связи, страница 10

   ………………………..

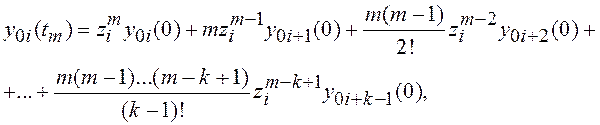
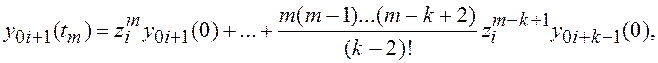Все слагаемые этой суммы при m→∞ также затухают, если выполняется условие (2.24). Таким образом, условие устойчивости линейной дискретной системы, описанной в пространстве состояний, формулируется следующим образом: для обеспечения устойчивости системы необходимо и достаточно, чтобы все собственные значения переходной матрицы по модули были меньше единицы.

          В качестве примера рассмотрим задачу анализа устойчивости дискретной системы 1-го порядка (рис. 1.36, а). Из уравнения (1.39) следует, что переходная матрица, характеризующая собственное движение системы, равна 1-KΔt. Записываем характеристическое уравнение системы: z-1+KΔt=0 и находим собственное значение переходной матрицы: z₁=1-KΔt. Из условия  определяем область допустимых значений параметра системы  обеспечивающих ее устойчивость:

          В разд. 1.13 представлено условие эквивалентности рассматриваемой дискретной системы и непрерывной системы с ПФ в разомкнутом состоянии :  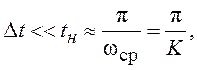откуда находим:   Воспользуемся уравнением (1.39) для анализа переходных процессов в дискретной системе (положим y(t₀)=0 и g(t_i+1)=1). Решение (1.44) для 3-х значений  показано на рис. 2.11. Поведение

дискретной и непрерывной систем очень похоже при  В случае  поведение дискретной системы весьма отличается от поведения непрерывной системы: если  переходный процесс в дискретной системе завершается за один такт Δt; если  переходный процесс в дискретной системе приобретает колебательный характер. Применение рассматриваемой дискретной системы в устройствах радиоавтоматики обычно предполагает выбор  при этом система не только имеет монотонный переходный процесс, но и обладает сглаживающими свойствами (см. гл. 3).

2.6. Алгебраический критерий устойчивости дискретных систем

          Если в характеристическом уравнении дискретной системы

                                            (2.25)

выполнить замену переменной z на w с помощью билинейного преобразования

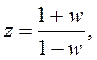                                                             (2.26)

то (2.25) преобразуется в характеристическое уравнение эквивалентной непрерывной системы (билинейное преобразование отображает круг единичного радиуса на плоскости комплексной переменной z в левую полуплоскость комплексной переменной w, являющейся аналогом комплексной переменной p=λ). Далее можно применить известные критерии устойчивости непрерывных систем (обычно используют критерий Рауса-Гурвица). При этом для систем 1-го и 2-го порядка достаточно воспользоваться необходимым условием устойчивости.

          Рассмотрим характеристическое уравнение дискретной системы 1-го порядка, имеющее, в общем случае, вид:

После подстановки (2.26) и простых преобразований получаем

Необходимое условие устойчивости требует положительности коэффициентов этого уравнения:

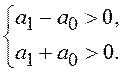
          Рассмотрим характеристическое уравнение дискретной системы 2-го порядка, имеющее, в общем случае, вид:

Замена переменной z на w с помощью (2.26) приводит к уравнению:

Необходимое условие устойчивости требует положительности коэффициентов этого уравнения:

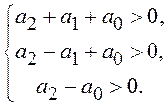
          Для систем более высокого порядка после замены переменной необходимо анализировать знаки определителей Гурвица. Так, для дискретной системы 3-го порядка с характеристическим уравнением  условия устойчивости определяет система неравенств:

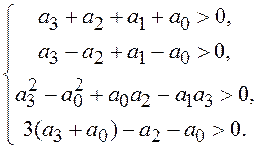
          В качестве примера рассмотрим задачу анализа устойчивости дискретной системы 2-го порядка (рис. 1.36, б). Переходная матрица:

Характеристическое уравнение системы:

Область допустимых значений параметров системы   и обеспечивающих ее устойчивость, определяет система неравенств:

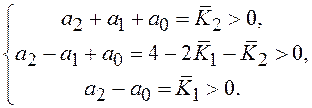
          Решение системы неравенств на плоскости параметров  и  располагается в области, ограниченной треугольником (рис. 2.12).

          Анализ собственных значений матрицы Φ (корней характеристического уравнения): 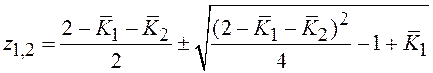 позволяет выявить область параметров, соответствующую апериодическим переходным процессам. Наиболее интересной для устройств радиоавтоматики является область параметров:  и . В этой области апериодические и колебательные переходные процессы разделяет линия (см. рис. 2.12), определяемая из условия  кратности собственных значений матрицы Φ: 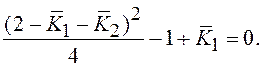 Область параметров, соответствующая апериодическим переходным процессам, на рис. 2.12 заштрихована.

           Если  и  переходный процесс в дискретной системе завершается за два такта Δt.