Устойчивость линейных систем. Критерий Рауса-Гурвица. Коррекция с помощью местной обратной связи, страница 9

          Включение в схему усилителя обеспечивает также уменьшение зоны нечувствительности статической характеристики привода. Линеаризация остальной части статической характеристики происходит за счет действия всех элементов коррекции. Действительно, тахогенератор является точным измерительным прибором, линейно преобразующим скорость вращения вала двигателя в напряжение. В схеме с обратной связью выполняется сравнение входного напряжения U_ВХ и напряжения тахогенератора U_Т. При большом значении коэффициента усиления  для вращения двигателя достаточно иметь малое значение разности U_ВХ-U_Т. Следовательно, U_ВХU_Т и, благодаря линейности характеристики тахогенератора, скорость вращения вала привода пропорциональна U_ВХ.

          Заметим, что в рассмотренной схеме коррекции привода меняется (уменьшается) коэффициент усиления. Иногда на выходе тахогенератора включают RC-цепочку (рис. 2.6, г) с ПФ 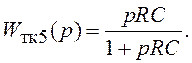    В этом случае условие  меняется на обратное не только с увеличением, но и с уменьшением частоты и, в соответствии с (2.19), в низкочастотной области  (обратная связь не действует). При этом сохраняется высокий коэффициент усиления привода, равный KK_дв.

          В задачах проектирования цифровых систем используют дискретный эквивалент скорректированной аналоговой системы, либо применяют дискретные эквиваленты корректирующих элементов, описываемых разностными уравнениями.

2.5. Условие устойчивости дискретных систем

          Рассмотрим однородное разностное уравнение системы n-го порядка:

                                     (2.20)

где Φ – переходная матрица.

          С помощью линейного преобразования Y(t_i)=ΛY₀(t_i) с неособенной матрицей Λ можно от (2.20) перейти к уравнению

                                   (2.21)

где матрица Φ₀=Λ^-1ΦΛ имеет, в общем случае, жорданову форму.

          Числа z₁, z₂, …, z_n, расположенные на главной диагонали Φ₀, называются собственными значениями матрицы Φ. Подстановка этих чисел в матрицу (zI-Φ) превращает ее в вырожденную матрицу с нулевым определителем:

                    (2.22)

Левая часть (2.22) называется характеристическим многочленом матрицы Φ (матрицы Φ и Φ₀=Λ^-1ΦΛ подобны и имеют один и тот же характеристический многочлен), а само уравнение (2.22) называется характеристическим уравнением дискретной системы, описываемой уравнением (2.20).

          Таким образом, собственные значения переходной матрицы Φ – z₁, z₂, …, z_n – определяются в результате решения характеристического уравнения (2.22).

Если все собственные значения z₁, z₂, …, z_n различны, то переходная матрица дискретной системы, описываемой уравнением (2.21), имеет диагональную форму: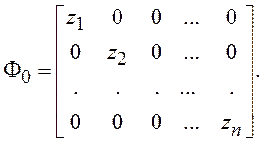

          При этом нетрудно найти решение уравнения (2.21) для произвольного дискретного времени t_m:

                                             (2.23)

 причем 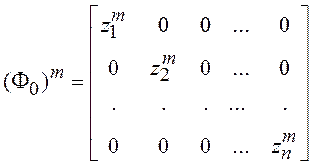 и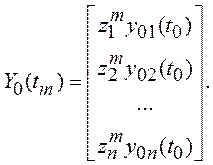

          Аналогично результату (2.5), решение уравнения (2.20) представляет собой вектор Y(t_m), элементами которого являются взвешенные суммы вида 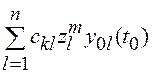 (c_kl – элементы матрицы Λ; k=1,2,…,n).

          В устойчивой системе все элементы вектора Y(t_m) должны  стремиться к нулю при m→∞. Это условие выполняется, если

                                              (2.24)

          К этому же результату можно прийти, рассматривая дискретную систему, описываемую уравнением (2.20), в качестве дискретного эквивалента непрерывной системы, матрица которой F имеет собственные значения λ₁, λ₂, …, λ_n. Как показано в разд. 2.1, при выполнении декомпозиции системы переходная матрица приобретает диагональную форму с элементами  на главной диагонали (Δt – интервал временной дискретизации). Отображение  преобразует левую полуплоскость комплексной переменной λ (область устойчивости непрерывной системы) в круг единичного радиуса на плоскости комплексной переменной z (область устойчивости дискретной системы). Заметим, что кругу единичного радиуса на плоскости комплексной переменной z соответствует часть левой полуплоскости комплексной переменной λ, лежащая между двумя горизонтальными прямыми Jm{λ}=ω₀ и Jm{λ}=ω₀+2π/Δt при произвольной ω₀; при этом одному обходу единичной окружности точкой z соответствует перемещение точки λ от одной горизонтальной прямой к другой.

          Если  среди z₁, z₂, …, z_n имеются кратные собственные значения переходной матрицы, то для собственных значений z_i кратности k жордановой клетке

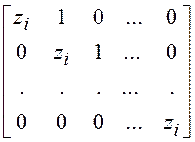 сопоставляется ее m-я степень

 вида: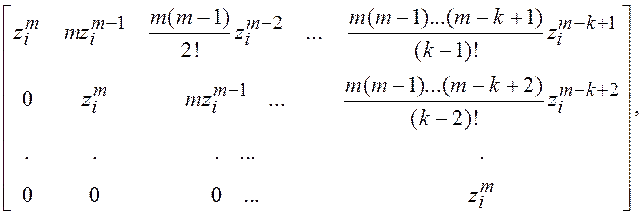

поэтому строки с индексами i, i+1,…,i+k-1 в решении (2.23) заменяются суммами: