Остальные параллели и меридианы изображаются кривыми и искажаются, причём, более всего – у краёв зоны (до 0.001 длины линии, измеренной на карте).
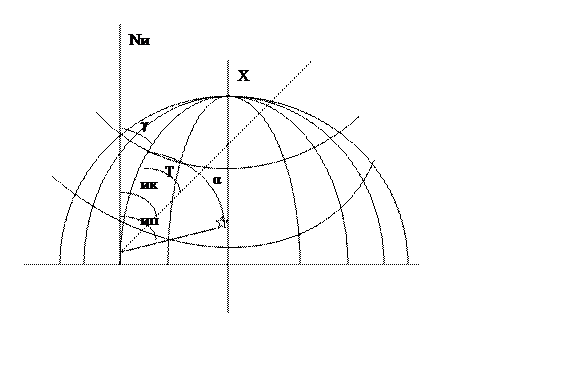
Такие искажения при практической работе неощутимы, поэтому, масштаб любого участка карты считается постоянным (на сравнительно небольших участках рек и водохранилищ – несколько сантиметров на 1 километр). Курс изображается прямой линией. Осевой меридиан принимается за ось Х, экватор – за ось У, следовательно, вся проекция строится в системе прямоугольных плоских координат. В зонах наносится координатная сетка, линии которой отстоят друг от друга на целое число километров, поэтому она называется километровой. Зона делится на листы карт. Все направления на картах – от вертикальных линий сетки. Угол между северной частью вертикальной линии координатной сетки и носовой частью ДП судна называется дирекционным курсом и обозначается Т. Угол между северной частью вертикальной линии координатной сетки и направлением на пеленгуемый объект называется дирекционным углом и обозначается α. Угол между ИМ данной точки и вертикальной линией координатной сетки называется углом схождения меридианов и обозначается γ.
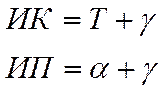
![]()
где ![]() - долгота места.
- долгота места.
![]() - долгота осевого меридиана.
- долгота осевого меридиана.
φ – широта места.
Угол между магнитным меридианом и вертикальной линией называется ориентирным углом и обозначается Δ.
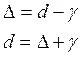
Сведения о величине и знаке ориентирного угла Δ, магнитного склонения d и γ помещены в виде схемы на полях карты водохранилища.
Формулы для решения задач на исправление и перевод направлений в проекции Гаусса:
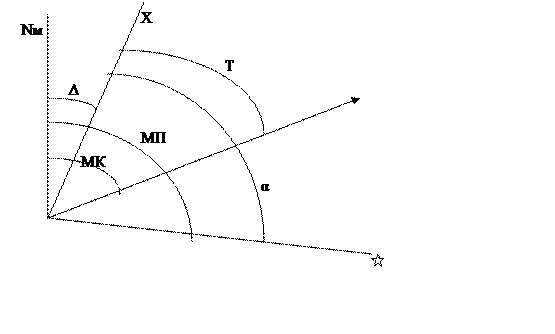
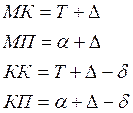
Требования к МНК. Меридиональная часть. Локсодромия и анализ её уравнения. Теория и свойства Меркаторской проекции. Масштаб карты, единица карты. Построение карты. Классификация морских карт. Оценка достоинства МНК.
Элементарная теория Меркаторской карты:

Из
треугольника ОВС: ![]()
![]()
![]()
т.е. при проектировании сфероида на цилиндр происходит растяжение каждой параллели пропорционально секансу её широты, отсюда, чтобы сохранить на карте подобие очертаний предметов (равноугольность), необходимо вытянуть на столько же и меридианы.
Требования к МНК:
· Путь судна, идущего постоянным курсом, т.е., пересекающего все меридианы под определённым углом, должен изображаться прямой.
· Углы, измеряемые на местности (курс, пеленг), должны быть равны соответствующим углам на карте.
· Если курс равен 0 или 180°, то он совпадает с меридианом, следовательно, и меридиан должен изображаться прямой, параллельной такому курсу. По той же причине экватор и параллели должны изображаться прямыми, параллельными между собой.
Локсодромия («косой бег»).
Если судно совершает переход одним и тем же курсом, то его путь на поверхности Земли изображается линией двоякой кривизны – локсодромией. Она представляет из себя логарифмическую спираль и пересекает все меридианы под одним и тем же углом, стремясь к полюсу, но никогда его не достигая (при условии, что курс не равен 0 или 180°). На меркаторской карте локсодромия изображается прямой, которая не выражает кратчайшего расстояния между 2 точками на земной поверхности. Уравнение локсодромии необходимо для получения точного выражения МЧ.
По Сакеллари:
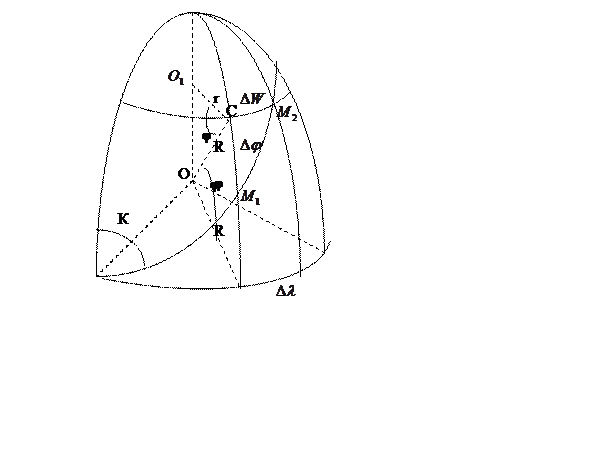
Считая Землю сферой, выберем на ней 2 меридиана с
разностью долгот Δλ. На этих меридианах отложим 2 точки ![]() и
и![]() с бесконечно малой разностью широт Δφ.
Проведя через т.
с бесконечно малой разностью широт Δφ.
Проведя через т. ![]() параллель, получим прямоугольный
треугольник
параллель, получим прямоугольный
треугольник ![]() . Из треугольника
. Из треугольника ![]() радиус
этой параллели:
радиус
этой параллели: ![]() . Из этого выражения следует, что
длина любой параллели равна длине экватора, умноженной на cosφ
(
. Из этого выражения следует, что
длина любой параллели равна длине экватора, умноженной на cosφ
(![]() ).
).
Для отрезков параллели и экватора соблюдается то же соотношение:
![]()
Поскольку треугольник ![]() элементарно
мал, его можно считать плоским, тогда:
элементарно
мал, его можно считать плоским, тогда: ![]() ,
откуда:
,
откуда:
![]()
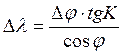
переходя к дифференциалам, получим:
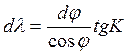
По учебнику:
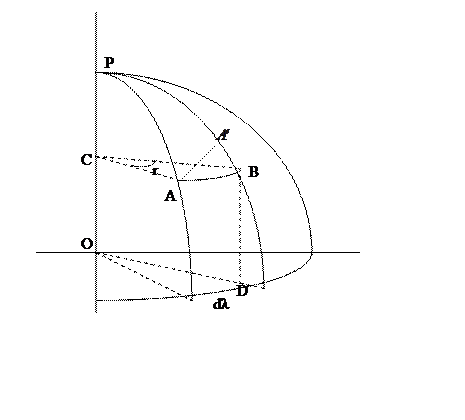
![]()
Элемент локсодромии ![]() настолько
мал, что треугольник
настолько
мал, что треугольник ![]() можно принять за плоский. Угол
можно принять за плоский. Угол ![]() представляет из себя курс судна.
представляет из себя курс судна.
![]()
![]() - разность долгот точек
- разность долгот точек ![]() и
и ![]() ,
радиан.
,
радиан.
![]()
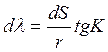 (3)
(3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.