Расчет сборных железобетонных конструкций промышленного здания, длинна которого равна 144 метрам (место строительства – г. Чита), страница 9

от температурного перепада (при ∆t=65°):

σ₂=1,25×∆t

σ₂=81,25 МПа

от деформации анкеров у натяжных устройств при длине арматуры l=25 м:

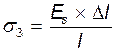
σ₃=30,02 МПа

где ∆l=1,25+0,15×d=3,95 мм.

Усилие обжатия бетона с учетом потерь σ₁, σ₂, σ₃ при коэффициенте точности напряжения γ_sp=1:

P₁= γ_sp×A_sp×( σ_sp- σ₁-σ₂-σ₃)=1137,83 кН

Эксцентриситет действия силы P₁:

e_op=y₀-a

e_op=117,06 см

Расчетный изгибающий момент в середине балки от собственного веса, возникающий при изготовлении балки в вертикальном положении, кНм:

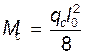
M_c=473,38 кНм

Нормативный изгибающий момент в середине балки от собственного веса, возникающий при изготовлении балки в вертикальном положении:

M_cⁿ=M_c/1,1=430,35 кНм

Напряжение обжатия бетона на уровне центра тяжести напрягаемой арматуры от действия усилия P₁ и момента M_nc

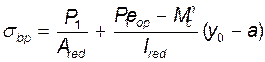
σ_bp =5,3 МПа

σ_bp/R_bp=0,272<0,75

Потери напряжений от быстронатекающей ползучести для бетона, подвергнутого тепловой обработке:

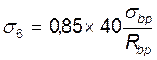
σ₆=9,25 МПа

Первые потери:

σ_los1= σ₁+ σ₂+ σ₃+ σ₆

σ_los1=142,83 МПа

Вторые потери: от усадки бетона класса В30, подвергнутого тепловой обработке при атмосферном давлении σ₈=30 МПа, от ползучести бетона

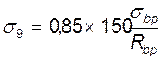
σ₉=34,7 МПа

Суммарное значение вторых потерь:

σ_los2= σ₈+ σ₉

σ_los1=64,7 МПа

Полные потери предварительного напряжения арматуры:

σ_los= σ_los1+ σ_los2

Усилие обжатия бетона с учетом полных потерь:

P₂=A_sp×( σ_sp- σ_los)=836,68 кН

Расчет по образованию трещин, нормальных к оси балки

Расчет по образованию трещин, нормальных к оси балки выполняют для выяснения необходимости проверки по раскрытию трещин. В этом расчете следует проверить трещиностойкость балки при действии эксплуатационных нагрузок (при γ_f>1) и при отпуске арматуры.

Расчет при действии эксплуатационных нагрузок:

Равнодействующая усилий обжатия бетона с учетом всех потерь при γ_sp=0,9:

P₀₂=P₂∙γ_sp

P₀₂=753 кН

Эксцентриситет равнодействующей P₀₂:

e₀=y₀-a

e₀=118,06 см

Момент сил обжатия относительно верхней ядровой точки:

M_rp=P₂×(r+e_op)

M_rp=1296,236 кНм

Момент, воспринимаемый сечением балки в стадии эксплуатации непосредственно перед образованием трещин в нижней части:

M_crc=R_bf,ser×W_pl+M_rp

M_crc=2029,26 кНм<M_c=2132 кНм

Следовательно, в растянутой зоне образуются трещины. Необходим расчет по раскрытию трещин. Изгибающий момент от длительной нагрузки M_l,ser=1843 кНм<M_cr=2029 кНм, поэтому можно проверить только кратковременное раскрытие трещин.

Необходимые вспомогательные величины для определения ширины кратковременного раскрытия трещин, нормальных к продольной оси балки в сечении 6-6:

h₀=h-a=225 см

M_ser=2132 кНм

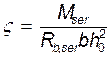=0,191

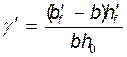=0,622

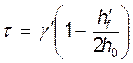=0,574

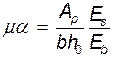=0,118

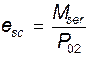=283,19

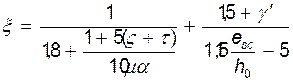=0,394

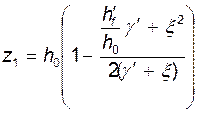=197,08 см

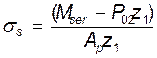=80,798 МПа

Ширина кратковременного раскрытия трещин:

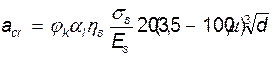=0,0452 мм< 0,15 мм

Расчет при отпуске напряжения арматуры:

Проверяем, образуются ли начальные трещины в верхней зоне балки при ее обжатии при значении коэффициента γ_sp=0,9. Усилие обжатия бетона при отпуске напряжения арматуры P₀₁=990,134 кН, Момент внутренних усилий в момент в момент отпуска натяжения

M'_crc=R_bt,serW’_pl-M_rp=-384,15 кН< M_cⁿ=430,35 кНм

Трещины в верхней зоне балки при γ_sp=0,9 не появляются.

При значении коэффициента γ_sp=1,1 будем иметь: P₀₁=1210,16 кН; M_rp=614,43 кНм; M’_crc=297,65 кНм< M_cⁿ=430,35 кНм, следовательно, и при γ_sp=1,1 в верхней зоне трещины не образуются.

Расчет по образованию наклонных трещин

За расчетное принимаем сечение на расстоянии 0,8 м от опоры, в котором сечение стенки уменьшается с 30 до 10 см. Высота балки в месте изменения сечения h=122,07 см. Поперечная сила от расчетной нагрузки Q=379,95 кН.

Геометрические характеристики сечения сведены в таблицу 7.

Таблица 7. Геометрические характеристики сечения