Максимальная поперечная сила у грани опоры Q×γn=407,75 кН. Размеры балки у опоры: h=101,87 см, h0=86,87 см, b=10 см (на расстоянии 0,8 м от торца), b=30 см на опоре. Вычисляем проекцию расчетного наклонного сечения на продольную ось с:
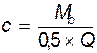
где:
![]()
влияние продольного усилия обжатия
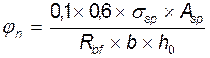
коэффициент учитывающий наличие полок тавровых сечений
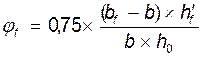
φf=0,656>0,5, принимаем φf=0,5
φn=0,0097
(1+φf+φn)=1,5097>1,5, принимаем 1,5
Mb=27166215 Н×см
В расчетном наклонном сечении Qb=Qsw=Q/2, отсюда:
c=133,25 см<2h0, с>h0, следовательно трещины будут начинаться у опоры
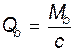
Qb=203,87 кН < Q=407,75 кН
По расчету требуется поперечная арматура. Принимаем для поперечных стержней арматуру ⌀8 A-III, Asw=0,503 см2. По конструктивным требованиям шаг поперечных стержней должен быть не более 1/3 h и не более 50 см. Принимаем предварительно на приопорных участках шаг поперечных стержней s=15 см. Усилие, воспринимаемое поперечными стержнями у опоры на 1 см длины балки:
qsw=Rsw∙Asw∙n/s=1911,4 Н/см
где n – число поперечных стержней в одном сечении.
qsw=1911,4>0,5φb3(1+φf+φn)Rbfb=540 Н/см.
Длина проекции опасной наклонной трещины на продольную ось балки:
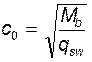
с0=119,22 см
Поперечное усилие:
Qsw=qsw×c0
Qsw=227,87 кН
Поперечная сила при совместной работе бетона и поперечной арматуры:
Qb,sw=Qb+Qsw
Qb,sw=431,75 кН>Qmax=407,75 кН
Прочность наклонного сечения обеспечена.
На остальных участках балки поперечные стержни располагаем в соответствии с эпюрой Q (рисунок 4.2).
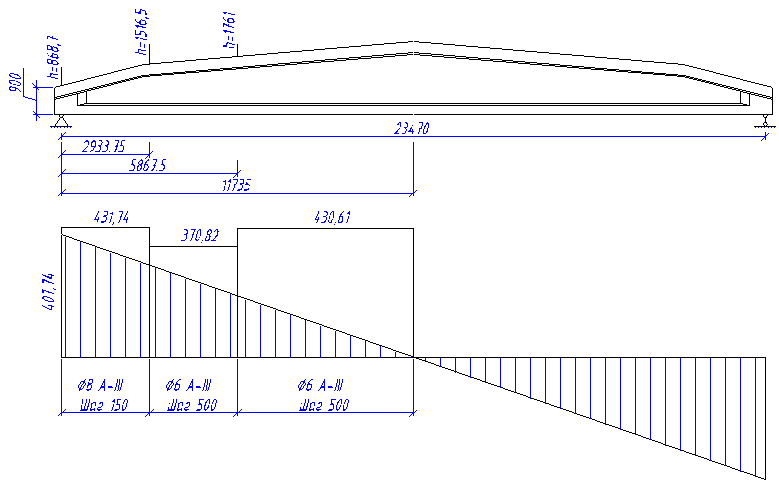
Рисунок Ошибка! Текст указанного стиля в документе отсутствует..9
Для средней половины пролета арматура ⌀6 A-III при h0=176,1 см и по конструктивным требованиям smax=50 см:
qsw=322,62 Н/см
с0=588,27 см >2×h0=352 см
Принимаем c=c0=352,2 см.
Qsw=113,63 кН
Qb=316,9875 кН
Qb,sw=430,617 кН >Qmax,mid=203,87 кН.
Для сечения в 1/8 пролета арматура ⌀6 A-III при h0=151,65 см и s=50 см:
qsw=322,62 Н/см
с0=506,58 см >2×h0=303,3 см
Принимаем c=c0=303,3 см.
Qsw=97,85 кН
Qb=272,97 кН
Qb,sw=370,82 кН >Qmax,1/8=305,8 кН.
Расчет по предельным состояниям второй группы
Определение геометрических характеристик сечения
Определение геометрических характеристик сечения 6-6 проходящего посередине пролета балки представлено в таблице 6.
Таблица 6. Определение геометрических характеристик сечения
|
αsp=Es/Eb= |
6,551724 |
|
α=Es/Eb= |
6,896551 |
|
Приведенная площадь арматуры, см2 αspAsp= |
266,7862 |
|
Приведенная площадь арматуры, см2 αA's= |
42,48275 |
|
Площадь приведенного сечения 6-6, см2 Ared= |
4769,268 |
|
Статический момент сечения относительно нижней грани, см3 Sred= |
634605,24 |
|
Расстояние от центра тяжести приведенного сечения до нижней грани, см y0=Sred/Ared= |
133,061323 |
|
Расстояние от центра тяжести приведенного сечения до верхней грани, см y'0=h-y0= |
106,938676 |
|
Момент инерции приведенного сечения относительно центра тяжести сечения, см4 Ired=I0+Aai2= |
36124810,5 |
|
Момент сопротивления приведенного сечения для нижней растянутой грани балки при упругой работе материалов, см3 Wred=Ired/y0= |
271489,937 |
|
Момент сопротивления приведенного сечения для верхней грани балки при упругой работе материалов, см3 W'red=Ired/y'0= |
337808,65 |
|
Расстояние от центра тяжести приведенного сечения до верхней ядровой точки, см r=φnWred/Ared= |
54,0786109 |
|
Расстояние от центра тяжести приведенного сечения до нижней ядровой точки, см rinf=φnWred'/Ared= |
67,288765 |
|
Влияние неупругих деформаций γ= |
1,5 |
|
Момент сопротивления сечения для нижней грани балки с учетом неупругих деформаций бетона, см3 Wpl=γ∙Wred= |
407234,9 |
|
Момент сопротивления сечения для верхней грани балки с учетом неупругих деформаций бетона, см3 W'pl=γ∙W'red= |
506712,98 |
Определение потерь предварительного напряжения
Первые потери: от релаксации напряжений арматуры
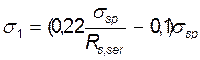
σ1=22,302 МПа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.