Расчет сборных железобетонных конструкций промышленного здания, длинна которого равна 144 метрам (место строительства – г. Чита), страница 10

Скалывающие напряжения на уровне центра тяжести:

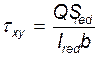=4,26 МПа

Напряжение в бетоне на уровне центра тяжести сечения от усилия обжатия при γ_sp=0,9:

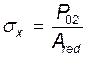=2,097 МПа

Поскольку поперечная напрягаемая арматура отсутствует σ_y=0. Главные растягивающие напряжения:

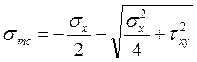=-5,438 МПа

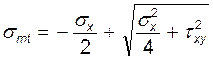=3,34 МПа

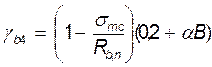=2,0786

Трещиностойкость по наклонному сечению обеспечена, так как R_bt,nγ_b4=3,74 МПа>σ_mt=3,34 МПа.

Определение прогиба балки

Прогиб балки определяем в сечении 6-6. Расчеты по определению прогиба балки сведены в таблицу 8, где:

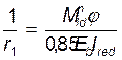-  , см^-2 – кривизна от постоянной и длительной нагрузки;

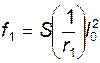-  , см – прогиб от постоянной и длительной нагрузки (S=5/48 при равномерно распределенной нагрузке);

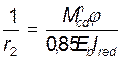-  , см^-2 – кривизна от кратковременной нагрузки (ϕ=1);

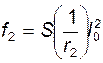-  , см – прогиб от кратковременной нагрузки (S=5/48 при равномерно распределенной нагрузке);

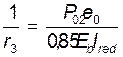-  , см^-2 – кривизна от усилий обжатия;

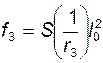-  , см – прогиб от усилий обжатия (S=1/8);

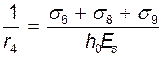-  , см^-1 – кривизна от усадки и ползучести бетона при отсутствии напрягаемой арматуры в верхней зоне сечения балки;

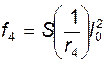-  , см – прогиб от усадки и ползучести бетона при отсутствии напрягаемой арматуры в верхней зоне сечения балки (S=1/8);

-  f_tot=f₁+f₂-f₃-f₄, см – полный прогиб балки.

Таблица 8. Определение прогиба балки

Расчет и конструирование сплошной колонны

По характеру действующих усилий колонны поперечной рамы относятся к внецентренно-сжатым элементам. Гибкие внецентренно-сжатые элементы при гибкости λ=l₀/i>14 рассчитывают с учетом эксцентриситета, получаемого умножением начального его значения e₀ на η>1. Площадь сечения каждого вида арматуры (A_s и A_s’) следует принимать не менее, чем 0,2% площади расчетного сечения бетона.

В проекте представлен расчет прочности сплошной колонны крайнего ряда (по оси А). Сечение арматуры подбираю по усилиям в сечении 2—2, поскольку там действуют наибольший по абсолютной величине момент М = - 199 кН•м при N=258 кН (комбинация 1+3+7+11+15 ). В это сочетание входят усилия от длительно действующей нагрузки М = -24 кН•м при N = 211 кН.

Так как в сочетание входят крановые нагрузки, расчетная длина надкрановой части колонны в плоскости изгиба по :l₀= 2Н= 2 х 4,4 = 8,8 м, а коэффициент условии работы бетона = 1.1

Характеристики бетона и арматуры

Бетон: тяжелый класса В20, подвергнутый тепловой обработке при атмосферном давлении; R_b=17 МПа; R_bt=1,2 МПа; с учетом  R_b=18,7 МПа; R_bt=1,32 МПа; E_b=29000 МПа.

Арматура: класса А-III, d>10 мм; R_s=R_sc=365 МПа; E_s=2×10⁵ МПа.

Надкрановая часть колонны

Размеры прямоугольного сечения надкрановой части b×h=0,4×0,6 м, a=a'=3 см. Полезная высота сечения h₀=0,57 м.

Эксцентриситет продольной силы е₀ =М/N= -199/258 = 0,77 м.

Найдем значение условной критической силы и величину коэффициента η для учета влияния прогиба элемента на величину эксцентриситета продольной силы. .
По п. 3.24 [2] определяю моменты относительно центра тяжести арматуры  А_s