Методические указания по выполнению контрольных работ по дисциплинам "Начертательная геометрия", "Инженерная графика", "Начертательная геометрия. Инженерная графика" и "Инженерная и компьютерная графика", страница 9

Из фронтальных проекций точек 1₂, 2₂, 3₂ проводим линии связи, перпендикулярно оси Х₂₄ и на них откладываем расстояния, равные расстояниям от горизонтальных проекций 1₁, 2₁, 3₁ до оси Х основной системы, т.е. координаты y этих точек.

Соединяем прямыми линиями полученные проекции точек 1₄, 2₄, 3₄ – получим натуральную величину сечения.

3.2.3 Комплексные задачи

Цель задачи – научится строить проекции плоских фигур, произвольно расположенных в пространстве.

Для выполнения задачи необходимо вспомнить разделы элементарной геометрии, касающиеся параллельности и перпендикулярности прямых и плоскостей, а также понятия о геометрических местах точек.

Следует проработать темы курса «Начертательная геометрия»: «Взаимное положение прямых», «Перпендикулярность прямых», «Пересечение прямой и плоскости».

Необходимо выполнить решение следующих элементарных задач:

1)  построить прямую, перпендикулярную плоскости;

2)  построить плоскость, перпендикулярную прямой;

3)  найти точку пересечения прямой и плоскости;

4)  разделить отрезок в заданном отношении;

5)  определить натуральную величину отрезка, занимающего общее положение.

Этот тип задач относится к комплексным, т.е. состоит из ряда элементарных позиционных (построение взаимно перпендикулярных и взаимно параллельных прямых, нахождение точки пересечения прямой и плоскости и т.д.). При решении задач этого типа основное затруднение вызывает правильный анализ и составление затем плана решения на основе пространственных представлений и теоретических оснований элементарной геометрии.

В качестве общего подхода к решению таких задач можно рекомендовать следующий. На отдельные элементы искомой фигуры (одну из вершин плоской фигуры) наложен ряд условий. Каждому такому условию удовлетворяет множество точек. Каждое из таких множеств может быть представлено геометрической фигурой. Некоторый элемент, удовлетворяя одновременно всем заданным условиям, должен принадлежать пересечению рассмотренных множеств, т.е. является пересечением соответствующих им геометрических фигур. На основе такого анализа составляется план решения в пространстве, в котором описывается, как, последовательно определив отдельные элементы искомой геометрической фигуры и зная её свойства, можно достроить всю фигуру.

Построения на чертеже, опираясь уже на основные положения начертательной геометрии, шаг за шагом отражают намеченные действия в пространстве.

Так, признаком перпендикулярности двух прямых в пространстве является перпендикулярность одной из прямых к плоскости, в которой находится вторая прямая. На чертеже такую плоскость целесообразно задать двумя пересекающимися прямыми, одна из которых является горизонталью, а другая – фронталью, так как, согласно свойству частного случая проецирования прямого угла, угол между заданной прямой и каждой из этих прямых проецируется без искажения на соответствующие плоскости проекций.

Если в пространстве не представляет труда определить точку пересечения прямой и плоскости, то для решения задачи на чертеже необходимо осуществить ряд вспомогательных операций, описываемых алгоритмом, рис. 10.

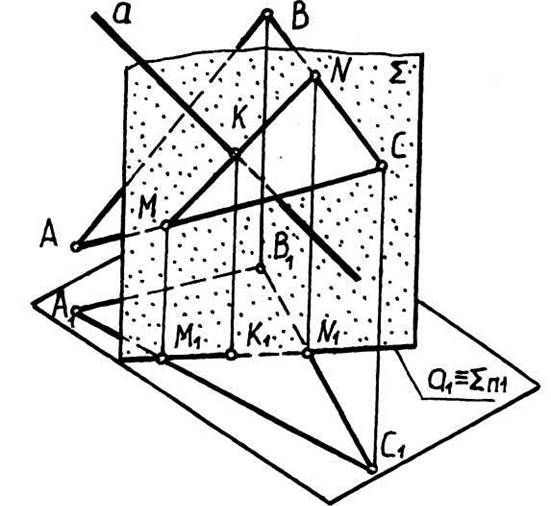
Рис. 10

Для построения точки пересечения прямой а с плоскостью ∆ следует:

1)  заключить заданную прямую а в плоскость-посредник S: SÎа;

2)  найти прямую пересечения MN плоскости S с данной плоскостью ∆(ABC): MN=Sg∆;

3)  на пересечении построенной прямой пересечения MN и данной прямой а найти искомую точку K: K=MNga.

При этом удобно заключить прямую а в проецирующую плоскость, так как сокращаются графические построения, а именно: как след плоскости S, так и одна из проекций вспомогательной прямой MN совпадает с одноименной проекцией данной прямой а благодаря инвариантному свойству соответствующей проекции проецирующей плоскости.

При выполнении третьего пункта данного алгоритма может встретиться такой случай, при котором легко определяется проекция только одной из точек вспомогательной линии MN, а проекция второй точки выходит за пределы чертежа. В этом случае на известной проекции вспомогательной прямой MN следует взять произвольную точку вместо той точки, вторую проекцию которой определить в пределах чертежа невозможно. Недостающую проекцию произвольной точки следует находить из условия принадлежности её плоскости, заданной горизонталью и фронталью.