Методические указания по выполнению контрольных работ по дисциплинам "Начертательная геометрия", "Инженерная графика", "Начертательная геометрия. Инженерная графика" и "Инженерная и компьютерная графика", страница 7

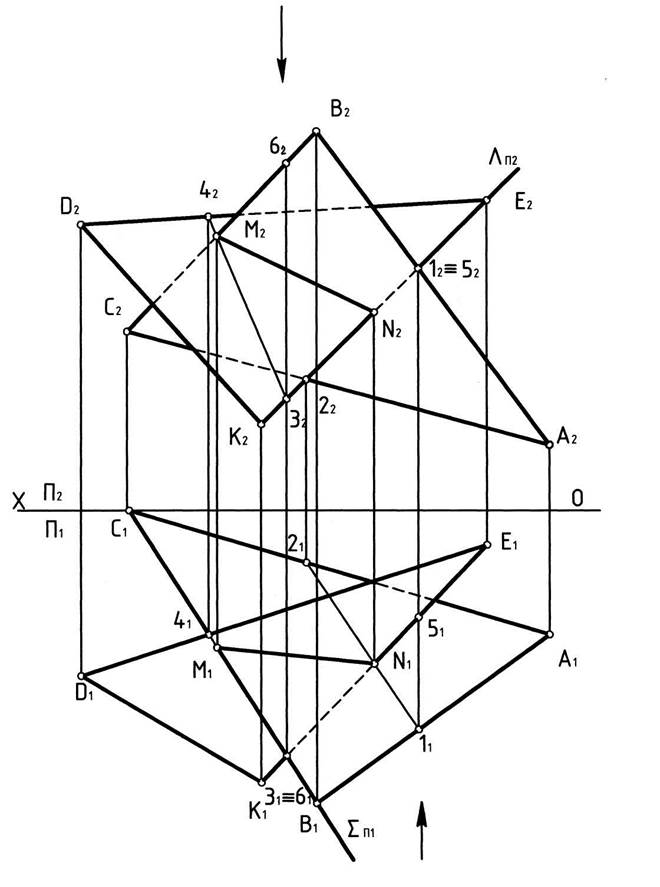
2.  Горизонтальную проекцию прямой 12 определяем из условия её принадлежности плоскости треугольника АВС: 1₂Y1₁ÎА₁В₁; 2₂Y 2₁ÎA₁C₁.

3.  Определяем горизонтальную проекцию точки пересечения горизонтальной проекции стороны KE и полученной прямой 12: N₁=K₁E₁g1₁21. По горизонтальной проекции точки N(N₁) находим её фронтальную проекцию N₂. Это и будет одна из точек, принадлежащих линии пересечения плоскостей.

4.  Повторяем те же операции для определения второй точки, принадлежащей искомой линии пересечения:

SÎBС; S^П₁YS_П1≡В₁С₁; S_П1 gD(АВС)=ВС; S_П1gW(DEK)=34; 3₁4₁≡S_П1;

3₁4₁Y 3₂4₂; M₂=3₂4₂gВ₂С₂.

5.  Соединяя одноимённые проекции точек M и N, получаем проекции искомой линии пересечения плоскостей MN (M₁N₁, M₂N₂).

6.  Видимость треугольников на фронтальной плоскости проекции определяем, например, по конкурирующим точкам 1 и 5, для которых 1₂≡5₂. Так как y₁>y₅, точка 1 находится ближе к наблюдателю, следовательно, прямая АВ закрывает прямую KE на плоскости П₂.

7.  Видимость треугольников на горизонтальной плоскости проекции определяем, например, по конкурирующим точкам 3 и 6, для которых 3₁≡6₁. Так как z₆>z₃, точка 6 расположен выше точки 3, следовательно, прямая ВС закрывает прямую КЕ на плоскости П₁.

3.2.2.2. Определение точки пересечения  прямой  с поверхностью тора

Цель задачи – научиться строить проекции точек пересечения прямой с поверхностью. Для этого следует уметь:

1)  задавать точку на поверхности;

2)  строить линии сечения поверхности плоскостью.

Рис. 7

Перед выполнением задания следует проработать тему «Определение точек пересечения линии и поверхности».

Правило построения точки пересечения линии и поверхности основано на общем приёме, состоящем в том, что данную линию заключают во вспомогательную плоскость-посредник D, строят линию пересечения её с заданной поверхностью и определяют точки пересечения полученной линии с заданной.

Если данная линия – прямая, то в качестве вспомогательной поверхности следует выбирать простейшую – плоскость. Прямую можно заключить во множество различных плоскостей,  причём лишь одну – горизонтально- проецирующую и множество – общего положения. Выбор плоскости-посредника зависит от трёх условий: вида заданной поверхности, взаимного расположения прямой и поверхности и их положения относительно плоскостей проекций. Рекомендуется вводить вспомогательную плоскость так, чтобы линия пересечения её с данной поверхностью проецировалась в виде простейших линий – прямых и окружностей, а это требует, прежде всего, знания формообразования поверхностей, умения выделять на заданной поверхности такие линии. Так, например, для цилиндрической или конической поверхности одним из множеств простейших линий является семейство прямых – образующих. Следовательно, можно ввести такую плоскость-посредник, которая пересечёт эти поверхности по образующим. Для этого она должна быть параллельна образующим цилиндрической или проходить через вершину конической поверхности. Если невозможно подобрать плоскость, пересекающую поверхность по простейшим линиям, то прямую следует заключить в проецирующую плоскость. Графическое удобство такого выбора в том, что сразу будет известна одна проекция линии пересечения. Она принадлежит соответствующему следу проецирующей плоскости. Другую проекцию линии следует искать из условия принадлежности её точек заданной поверхности. Видимость прямой по отношению к поверхности устанавливают на основе рассмотрения конкурирующих точек пересекающихся фигур, т.е. точек, лежащих на одной проецирующей прямой.

На чертеже заданы проекции прямой а – общего положения и поверхности тора с осью i, рис. 8. Заключим данную прямую в какую-либо проецирующую плоскость.

Выполним следующие построения на чертеже:

1.  Заключаем прямую а в плоскость D, проведя её след D_П2≡а_2.

2.  Находим проекции линии пересечения b плоскости D с поверхностью тора. Так как D^П₂, то b₂≡D_П2. Горизонтальную проекцию b₁ строим из условия принадлежности линии bповерхности тора.

3.  На пересечении фронтальных проекций a₁ и b₁ находим проекции M₁ и N₁, а затем M₂ и N₂.