3. ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ПО РАЗДЕЛУ «НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ»
3.1 Содержание заданий
Условия задач и числовые данные для каждого варианта выдаются преподавателем.
3.2 Методические указания к решению задач по «Начертательной геометрии»
Задачи, решаемые графическим путём с применением правил начертательной геометрии, можно отнести к трём типам: позиционные (определение общих элементов и взаимного расположения фигур), метрические (определение расстояний и углов) и комплексные задачи.
3.2.1 Метрические задачи
Метрическими называются задачи, в которых приходится определять значения измеряемых величин – измерять расстояния между двумя точками и величину угла между двумя прямыми.
Цель задач – научиться определять действительные размеры геометрических фигур по их проекциям без использования и с использованием способов преобразования чертежа. При использовании способов преобразования чертежа необходимо чётко понимать цель данных преобразований, – какое частное положение должна занять проецируемая геометрическая фигура в результате этих преобразований, а в зависимости от этого и проводить эти преобразования.
Для выполнения заданий следует вспомнить определения правила элементарной геометрии, касающиеся нахождения расстояний между точками, точкой и прямой, точкой и плоскостью и углов между плоскостями, между прямой и плоскостью, а также проработать темы начертательной геометрии: «Способы преобразования чертежа», «Метрические задачи».
Следует приобрести навыки решения следующих элементарных задач:
1) преобразовать чертёж прямой общего положения в чертёж прямой частного положения (параллельной плоскости проекций или проецирующей);
2) преобразовать чертёж плоскости общего положения в чертёж плоскости частного положения (проецирующей или параллельной плоскости проекций;
3) построить проекции прямых, с помощью которых определяются углы наклона плоскости к плоскостям проекций;
4) определить натуральную величину отрезка прямой;
5) построить проекции прямой, перпендикулярной плоскости;
6) найти точку пересечения прямой с плоскостью.
Решение задач на определение расстояния между двумя геометрическими фигурами сводится к решению простейшей задачи – определению расстояния между двумя точками, т.е. к определению длины отрезка, соединяющего эти точки.
Решение задач на определение угла между двумя геометрическими фигурами сводится к решению простейшей задачи – определению угла между двумя пересекающимися прямыми. Если этот отрезок или плоский угол параллельны какой-либо плоскости проекций, то на эту плоскость они проецируются без искажения. Если они занимают общее положение, то следует либо преобразовать чертёж так, чтобы геометрические фигуры заняли частное положение, либо определить измеряемые величины согласно известным правилам.
При решении каждой метрической задачи, прежде всего, следует, опираясь на знания элементарной геометрии, представить, каким образом измеряется искомое расстояние или каким плоским углом измеряется угол между заданными геометрическими фигурами, а затем решать задачу указанным в условии способом.
3.2.1.1 Определение расстояния между скрещивающимися прямыми
Заданные прямыеa и b занимают в пространстве общее положение, рис. 2. Величина расстояния между скрещивающимися прямыми определяется величиной отрезка перпендикуляра, заключённого между параллельными плоскостями, которым принадлежат скрещивающиеся прямые. Эти плоскости называются плоскостями параллелизма. Если отрезок, определяющий искомое расстояние, распложен параллельно какой-либо плоскости проекций, то он на эту плоскость проецируется без искажения. Если же он занимает общее положение, то следует графически преобразовать чертёж таким образом, чтобы этот отрезок занял положение параллельное какой-либо плоскости проекций. Это можно сделать двумя последовательными заменами плоскостей проекций.
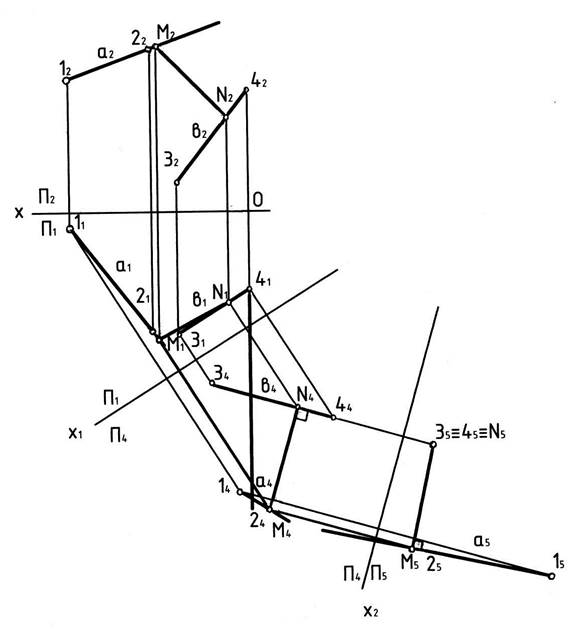
Рис. 2
Выполним следующие построения на чертеже:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.