Методические указания по выполнению контрольных работ по дисциплинам "Начертательная геометрия", "Инженерная графика", "Начертательная геометрия. Инженерная графика" и "Инженерная и компьютерная графика", страница 6

Как уже известно, величина угла наклона плоскости к какой-либо плоскости проекций определяется величиной угла между линией наклона к этой плоскости и её натуральной величиной. Известно, однако, что если заданная плоскость перпендикулярна к какой-либо плоскости проекций, то угол между её следом на эту плоскость и осью Х равен углу наклона заданной плоскости к другой плоскости проекций, В условии поставленной задачи плоскость треугольника является плоскостью общего положения. Следует повернуть эту плоскость вокруг фронтально-проецирующей прямой до положения, перпендикулярного П₁.

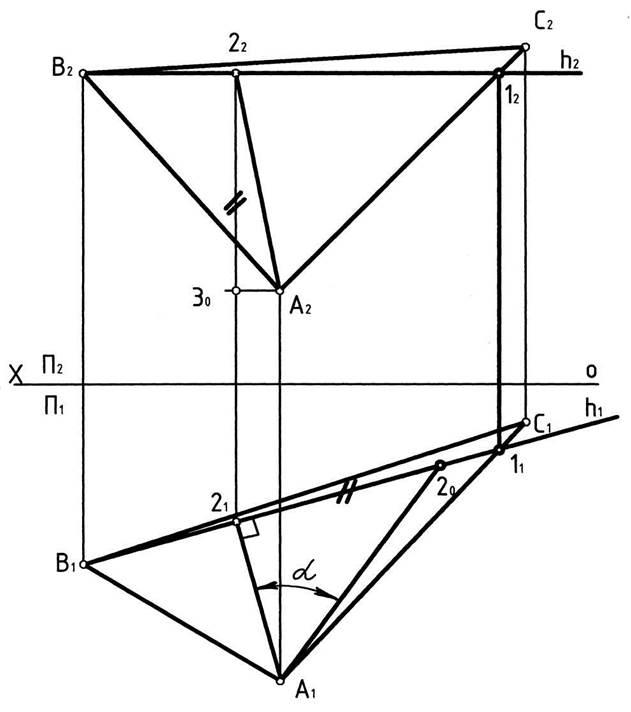
Рис. 4

За траекторию перемещения каждой точки берётся дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения. При этом на чертеже фронтальная проекция точки будет перемещаться по дуге окружности, горизонтальная – по прямой, параллельной оси проекций Х, рис. 5.

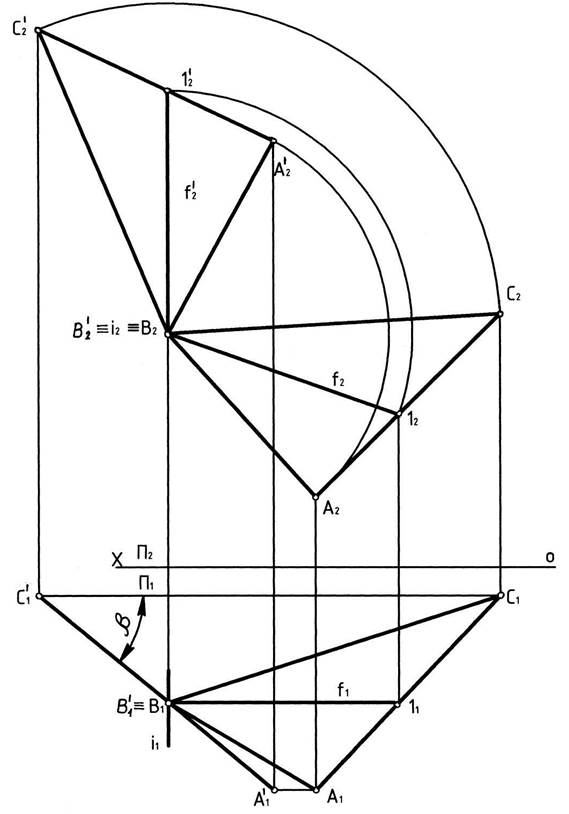
Рис. 5

Выполним следующие построения на чертеже:

1.  В плоскости треугольника проводим фронталь f: B₁Îf₁11X; f₁gA₁C₁=1₁; 1₁Y1₂ÎA₂C₂;f₂≡B₂1₂.

2.  Проводим ось вращения i: В₁Îi₁; i^П₂Y i₁^X.

3.  Поворачиваем фронталь вокруг оси вращения i до горизонтально-проецирующего положенияf^П₁: f′₂^X; |B′₂1′₂|=|B₂1₂|; |A′₂B′₂|=|A₂B₂|; |B′₂C′₂|=|B₂C₂|, |A′₂C′₂|=|A₂C₂|.

4.  Горизонтальные проекции точек перемещаются по прямым, параллельным оси проекций Х.

5.  На пересечении этих прямых и перпендикуляров к оси Х, проведённых из точек А′₂, В′₂, С′₂, находим новые горизонтальные проекции вершин треугольника А′₁, В′₁, С′₁.

6.  Соединяем одноимённые новые проекции вершин треугольника и получим новые его проекции.

7.  Так как новая горизонтальная проекция треугольника – прямая линия, то, следовательно, он занял горизонтально-проецирующее положение.

8.  Угол между (А′₁, В′₁ С′₁) и осью Х – искомый угол.

3.2.2 Позиционные задачи

К позиционным относятся задачи, решение которых, в конечном итоге, сводится к построению точки, принадлежащей линии, и к построению точки, принадлежащей поверхности.

3.2.2.1 Построение линии пересечения плоскостей D (АВС) и S (DEK)

Цель задачи – научиться строить проекции линии пересечения плоскостей. Для успешного решения этой задачи следует свободно владеть материалом по темам: «Пересечение прямой и плоскости», «Пересечение плоскостей».

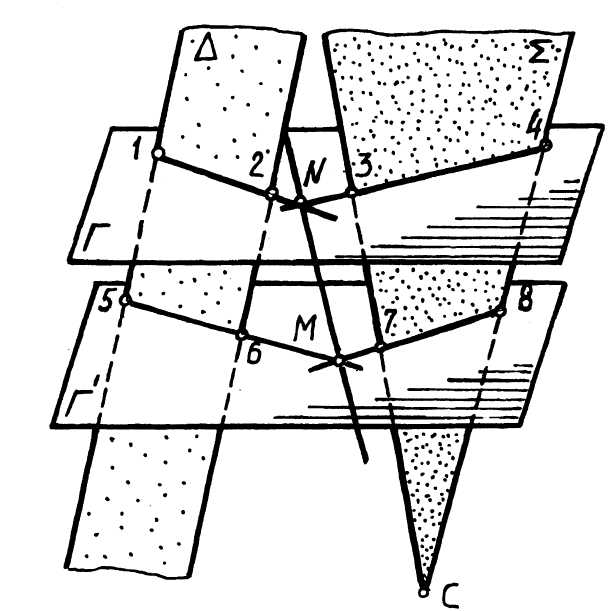
Две плоскости в общем случае пересекаются по прямой линии, точки которой одновременно принадлежат каждой из заданных плоскостей. Для построения линии пересечения следует определить две точки, общие для обеих поверхностей, рис. 6. Общим приёмом для нахождения точек, принадлежащих линии пересечения, является введение вспомогательных плоскостей­­- посредников согласно следующему правилу (алгоритму):

1)  ввести вспомогательную плоскость-посредник Г;

2)  построить линии пересечения этой плоскости с заданными D и S: ГgD=12; ГgS=34;

3)  найти точку пересечения найденных прямых линий N=12g34;

4)  найти точку М, повторив вышеперечисленные пункты алгоритма;

5)  соединить две  полученные точки  прямой и получить искомую линию пересечения плоскостей NM.

В качестве вспомогательных плоскостей-посредников рекомендуется выбирать проецирующие плоскости или плоскости уровня. В этом случае становится известной одна проекция линии пересечения вспомогательной плоскости-посредника и заданных плоскостей: она совпадает со следом вспомогательной плоскости. Вторую проекцию следует определять из условия её принадлежности заданным плоскостям.

На чертеже заданы две плоскости общего положения D(АВС) и W(DEK), рис. 7. Для построения линии их пересечения достаточно определит проекции двух точек, одновременно принадлежащих заданным плоскостям. Эти точки могут быть определены как точки пересечения сторон одного треугольника с плоскостью другого треугольника согласно правилу определения точки пересечения прямой и плоскости.

Рис. 6

Выполним следующие построения на чертеже:

1.  Заключаем сторону KE во вспомогательную фронтально-проецирующую плоскость-посредник Λ_П2. Эта плоскость пересекает заданный треугольник АВС по прямой 12, фронтальная проекция которой совпадает со следом плоскости Λ_П2  и с фронтальной проекцией стороны KE:  1₂2₂≡Λ_П2≡К₂E₂.