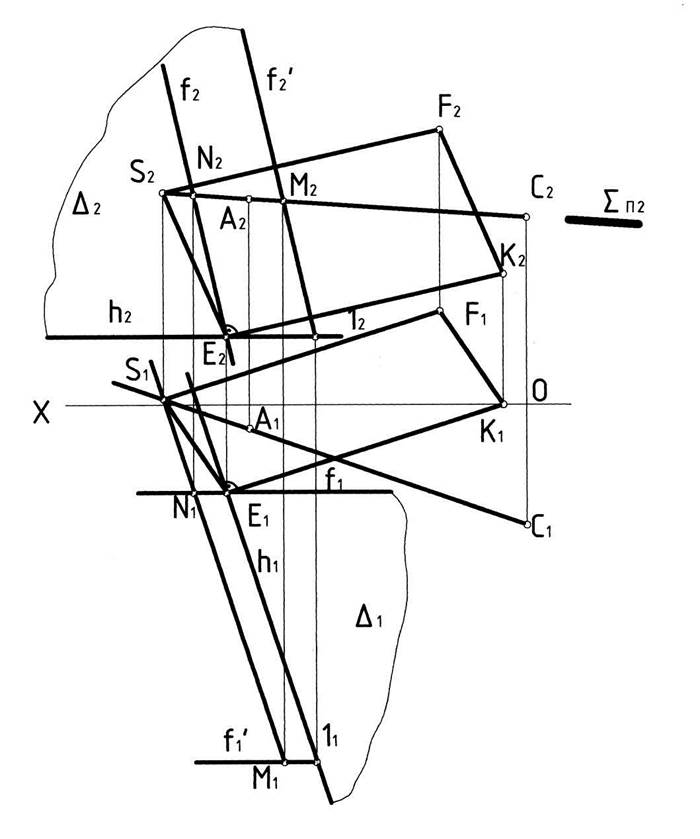
Рассмотрим решение задачи на построение проекции прямоугольника KESF, расположенного в плоскости Θ, если одной стороной служит прямая KE, а точка S принадлежит прямой AC, рис. 11.
По условию задачи заданы отрезки скрещивающихся прямых AC и KE. Оба отрезка – прямые общего положения.
По условию задачи на положение вершины S наложено два условия:
1) точка Sпринадлежит отрезку прямой АС. Этому условию удовлетворяет множество точек отрезка прямой AC;
2) точка S принадлежит стороне прямоугольника ES. Такому условию удовлетворяет множество точек плоскости ∆, перпендикулярной отрезку EK и проходящий через точку Е. Искомая точка S принадлежит пересечению указанных множеств (отрезка прямой KE к плоскости ∆).
Положение вершины F определяется как результат пересечения двух сторон параллелограмма, проходящих через известные вершины S и K, и параллельных известным сторонам прямоугольника EK и SE.
Алгоритм решения:
1. Провести через точку Е плоскость ∆ перпендикулярно отрезку EK: ∆ÎЕ и ∆^ЕК.
2. Определить точку пересечения прямой АС с плоскостью ∆: S=ACg∆;
3. Соединить точки Е и S.
4. Провести через точки S и K прямые SF11EK и KF11ES.
Выполним следующие построения на чертеже:
1. Проводим плоскость ∆, задавая её горизонтальюh и фронталью f, проходящими через точку Е, так, чтобы h1^E1K1 и f2^E2K2, согласно теореме о перпендикулярности прямой и плоскости.
2. Определяем проекции точки S (S1, S2) на основании общего алгоритма о пересечении прямой и плоскости, для чего заключаем отрезок прямой АС в плоскость-посредник S^П2, задавая её следом SП2≡А2С2; Находим фронтальную проекцию линии пересечения плоскостей ∆ и S, обозначив её MN. Фронтальный след плоскости SП2 пересекает фронтальную проекцию фронталиf в точке N, а фронтальную проекцию горизонтали hв точке, которая выходит за пределы чертежа. Для определения точки M берём точку 1 на горизонтали h и проводим дополнительную фронталь f1(f11, f21). Горизонтальную проекцию вершины S прямоугольника находим на пересечении прямых А1С1 и M1N1.
3. Соединяем одноимённые проекции точек S и E.
4. Через горизонтальные и фронтальные проекции точек S и K проводим проекции прямых, параллельные EK и SE соответственно. В точке их пересечении находим проекции вершины F (F1, F2).
3.2.4 Построение аксонометрических проекций геометрических фигур
Цель задания – научиться строить аксонометрические проекции геометрических фигур.
Для успешного выполнения этой задачи следует проработать теоретический материал «Аксонометрические проекции».
Для построения аксонометрической проекции плоской геометрической фигуры следует построить аксонометрические проекции точек, соединив которые, согласно обозначениям геометрической фигуры, получим искомую проекцию. Следует вспомнить, что, при построении изометрической проекции точки, коэффициенты искажения по аксонометрическим осям равны между собой. Для упрощения построения следует принимать коэффициенты по аксонометрическим осям, равные 1. Для упрощения построения диметрической проекции точки следует принимать коэффициенты искажения по осям X и Z, равные 1, а по оси Y – равный 0,5.
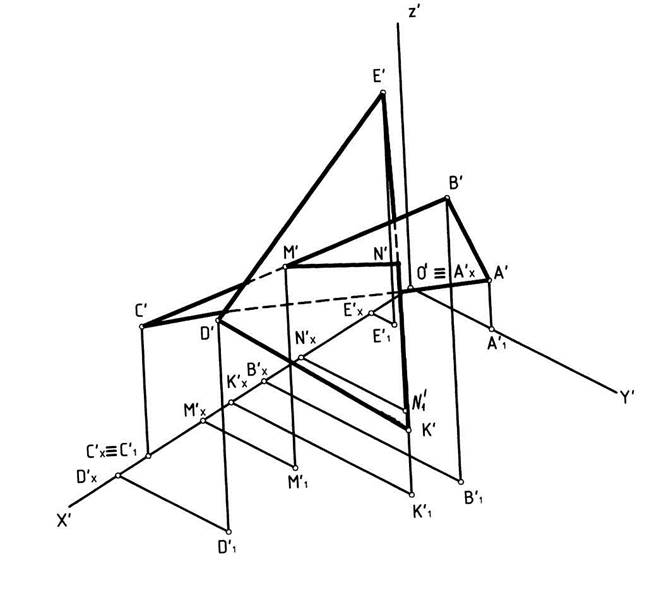
Рассмотрим построение прямоугольной изометрической проекции треугольников АВС и DEK и линии их пересечения, рис. 12.
Выполним следующие построения на чертеже:
1. Строим аксонометрические оси, откладывая угол между осями X′ и Y′, X′ и Z′ и осью Y′ и Z′ – 120°.
2. По заданным координатам строим аксонометрические проекции точек А, В, С. Для этого от начала координат следует отложить вдоль оси Х′, например, для точки А, координату ХА, далее через полученную точку АХ′ проводим прямую, параллельную оси Y′ и на ней откладываем отрезок, равный координате YA; через полученную точку проводим прямую, параллельную оси Z′ и на ней откладываем отрезок, равный координате ZA.
3. Аналогичным образом следует строить изометрические проекции всех вершин треугольников АВС и DEK.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.