1. Вводим дополнительную плоскость П411а (прямые aи b ограничиваем точками: a2≡ [1222], a1≡[1121], b2≡[3242], b1≡[3141]), П4^П1, П4gП1=X1, т.е. от системы Х П2\П1 переходим к системе Х1 П4\П1. При этом направление оси Х1 новой системы параллельно горизонтальной проекции прямой b1: Х111 b1.
2. Строим проекции прямыхa иb на плоскость П4. Для чего через 11, 21, 31, 41 проводим линии связи перпендикулярно Х1. Откладываем на них от оси Х1 расстояния, равные координате Z указанных точек, и строим новые проекции 14,24, 34, 44. Через них проводим новые проекции прямых a и b (a4 и b4).
3. Далее преобразуем чертёж таким образом, чтобы прямая b из линии уровня стала проецирующей прямой. Для этого вводим дополнительную плоскость П5^b; П5^П4 и П5gП4=Х2, т.е. от системы Х1П4\П1 переходим к новой системе Х2П4\П5. При этом направление оси Х2^b4.
4. Строим проекции прямых a иb на П5. Для этого через проекции 14, 24, 34, 44 проводим линии связи перпендикулярно оси Х2. Откладываем на них расстояния, измеренные от горизонтальных проекций точек (11, 21, 31, 41) до оси Х1, например, |15 X2| = |11 X1|. Так как эти расстояния для точек 3 и 4 равны и совпадают линии связи, то 35≡45, вследствие чего прямая b проецируется в точку, а прямая а – в прямую а5.
5. Поскольку отрезок, определяющий расстояние между прямыми a иb, перпендикулярен обоим заданным прямым, а одна из прямых (b) в системе плоскостей проекции Х2П4\П5 является проецирующей прямой, то, следовательно, искомый отрезок [М5N5] должен быть параллелен П5. Тогда прямой угол между искомым отрезком и прямой а на плоскость П5 проецируется без искажения. Из точки 35≡45 опускаем перпендикуляр на а5. Отрезок [M5N5] – искомое расстояние.
3.2.1.2 Определение углов наклона плоскости общего положения к плоскостям проекций без преобразования чертежа и способом вращения вокруг проецирующей прямой
Углы наклона плоскости общего положения к плоскостям проекции П1 и П2 определяются с помощью линий наибольшего наклона, рис. 3, рис. 4. Прямые, принадлежащие плоскости и перпендикулярные горизонталям (фронталям) плоскости, называются линиями наибольшего наклона к плоскостям П1 (П2).
Линия наибольшего наклона к плоскости П1 называется линией ската. Следовательно, чтобы построить линию наибольшего наклона к плоскости П1 (П2), следует в заданной плоскости построить горизонталь (фронталь), а затем через любую точку плоскости провести линию наибольшего наклона к П1 (П2). Линейный угол, между линией наибольшего наклона к плоскости П1 (П2) и её натуральной величиной равен углу наклона плоскости к плоскости проекций П1 (П2).
Для определения угла наклона плоскости общего положения, заданной треугольником ABC к плоскости проекций П2 выполним следующие построения на чертеже:
1. В плоскости треугольника ABC строим горизонтальную и фронтальную проекции фронтали: В1Îf111X1; f1gC1A1=11;f2≡B212.
2. Через фронтальную проекцию точки А проводим фронтальную проекцию линии наибольшего наклона к П2 перпендикулярно фронтальной проекции фронтали f: A222^f2.
3. Определяем натуральную величину линии наибольшего наклона. Для этого строим прямоугольный треугольник, одним катетом которого является фронтальная проекция этой линии, а другим – разность расстояний концов линии наибольшего наклона до плоскости П2, т.е. |2220|=|yА – y2|; |A220|=|A2|.
4. Замеряем величину линейного угла между фронтальной проекцией линии наибольшего наклона и её натуральной величиной. Это и будет искомый угол наклона плоскости треугольника к фронтальной плоскости проекции П2.
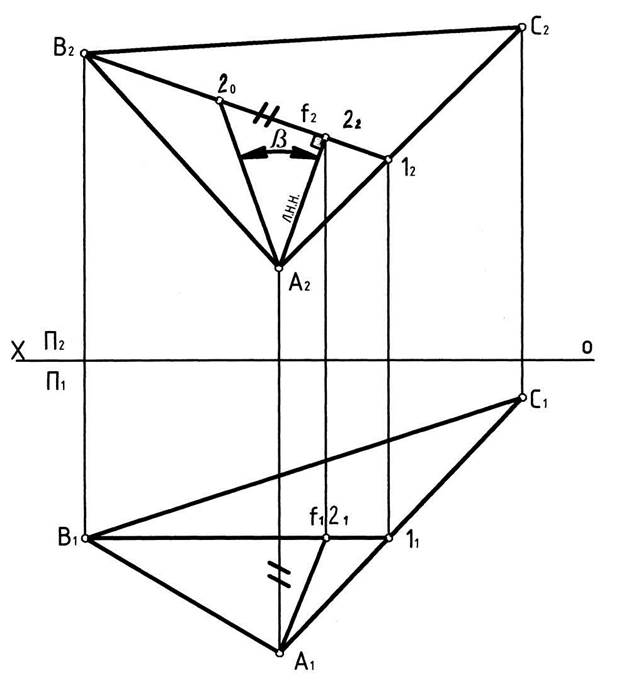
Для определения угла наклона плоскости треугольника АВС к плоскости проекций П1 следует построить проекции линии наибольшего наклона к плоскости П1, проведя её горизонтальную проекцию перпендикулярно горизонтальной проекции горизонтали.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.