Методические указания по выполнению контрольных работ по дисциплинам "Начертательная геометрия", "Инженерная графика", "Начертательная геометрия. Инженерная графика" и "Инженерная и компьютерная графика", страница 8

4.  Для определения видимости прямой а относительно поверхности тора при проецировании на П₁ воспользуемся конкурирующими точками, например, точкой 3, принадлежащей прямой а, и точкой D, принадлежащей поверхности тора, для которых D₁≡3₁. Т.к. точка 3 расположена выше точки D, т.е. z₃>z_D, то на горизонтальной плоскости проекций точка 3₁ закроет точку D₁. Следовательно, участок горизонтальной проекции прямой а до горизонтальной проекции точки пересечения прямой а с поверхностью тора (N₁) также будет видимый.

5.  Для определения видимости фронтальной проекции прямой а воспользуемся конкурирующими точками, например, 1Îа и 2, принадлежащей поверхности тора, для которых 1₂≡2₂. Так как точка I расположена ближе к наблюдателю, чем точка 2 (y₁>y₂), то фронтальная проекция точки 1(1₂) будет видимой, а фронтальная проекция точки 2(2₂) – невидимой. Следовательно, фронтальная проекция прямой а (а₂) до точки M₂ – фронтальной проекции точки пересечения прямой а с поверхностью тора, также будет видимой.

6.  Видимость остальных участков прямой а определяется аналогично.

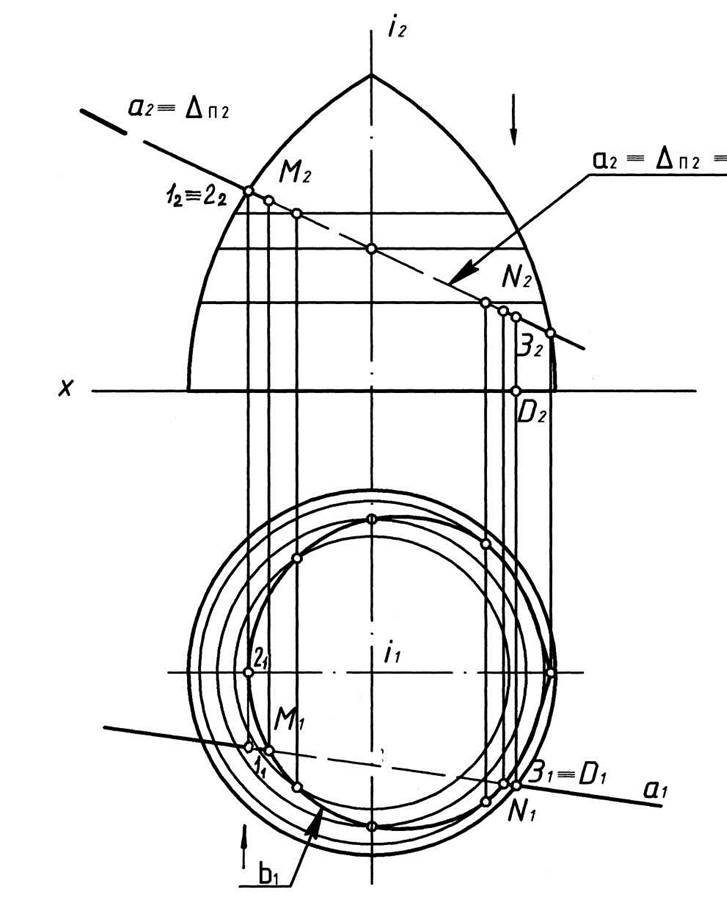
Рис. 8

3.2.2.3  Построение проекций и  натуральной величины линии сечения поверхности трёхгранной пирамиды  SABC  плоскостью S

Цель задачи – научиться строить проекции и натуральную величину сечения поверхности плоскостью.

Следует проработать теоретический материал: «Пересечение поверхности плоскостью».

Правило построения линии пересечения поверхности плоскостью основано на следующем:

1)  исходя из положения заданных геометрических фигур, следует определить вид линий пересечения;

2)  если заданная плоскость – проецирующая, то сразу известна одна проекция линии пересечения:  она совпадает со следом проецирующей плоскости;

3)  недостающие проекции искомой линии пересечения определяют из условия её принадлежности заданной поверхности;

4)  если обе заданные геометрические фигуры – общего положения, то следует способом замены плоскостей проекций преобразовать чертеж так, чтобы плоскость заняла проецирующее положение;

5)  для определения натурального вида сечения следует помнить, что геометрическая фигура проецируется на ту или иную плоскость проекций без искажения только в том случае, если её плоскость параллельна этой плоскости проекций.

Заданная на чертеже двумя проекциями пирамида SABC занимает в пространстве общее положение, рис. 9. Поскольку пирамида относится к многогранникам, следовательно, результатом её пересечения плоскостью будет многоугольник. Для построения проекций многоугольника достаточно определить проекции его вершин.

Заданная плоскость S - фронтально проецирующая. Следовательно, сразу имеется фронтальная проекция искомого многоугольника – она совпадает со следом заданной плоскости. Фронтальные проекции вершин искомого многоугольника будут совпадать с точками пересечения фронтального следа плоскости S с фронтальными проекциями рёбер пирамиды.

Недостающие проекции вершин многоугольника следует определять из условия их принадлежности соответствующим проекциям рёбер пирамиды.

Для определения натурального вида сечения пирамиды плоскостью следует использовать способ замены плоскостей проекций, введя новую плоскость проекций параллельно положению заданной плоскости D.

Выполним следующие построения на чертеже:

1.  Определяем фронтальные проекции вершин многоугольника: 1₂=S_П2gS₂A₂;  2₂=S_П2gS₂B₂;  3₂=S_П2gS₂C₂.

2.  Определяем горизонтальные проекции вершин многоугольника из условия принадлежности их горизонтальным проекциям соответствующих рёбер пирамиды:1₂Y1₁ÎS₁A₁; 2₂Y2₁ÎS₁B₁; 3₂Y3₁ÎS₁C₁;

3.  Определяем видимость геометрических фигур с помощью конкурирующих точек;

4.  Строим натуральную величину сечения пирамиды плоскостью S способом замены плоскостей проекций. От системы плоскостей проекций  х12 П₂/П₁ переходим к новой системе, в которой горизонтальную плоскость П₁ заменяем на новую П₄, при этом П₄^П₂ и П₄gП₂=Х₂₄. Для получения натуральной величины сечения следует ось Х₂₄ провести параллельно фронтальному следу плоскости S_П2.

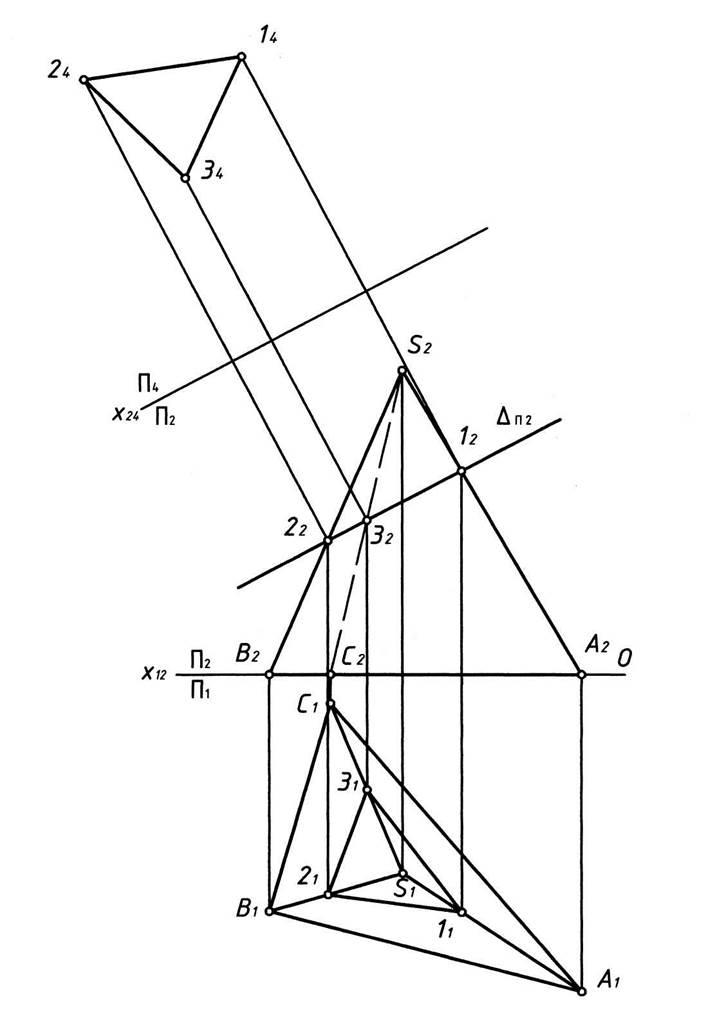
Рис. 9