Эксплуатационное обслуживание информационных систем железнодорожного транспорта, задание на контрольную работу № 2, страница 15

Для операций обработки информации

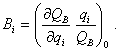                          (2.30)

Индекс 0 означает, что значения производных берутся в точке , принятой за начальную, где n, m – число операций обработки и контроля соответственно.

Для операций контроля ошибок в информации

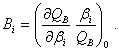                            (2.31)

Используя полученное ранее выражение для Q_B=Q₄, определим коэффициенты чувствительности для всех операций обработки и контроля информации:

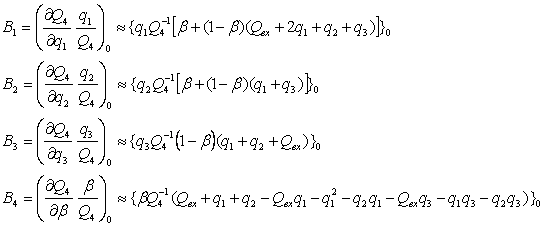
     (2.32)

Как следует из полученных значений коэффициентов чувствительности, на безошибочность выходной информации наиболее сильно влияет операция (3, 4).

Можно повысить безошибочность информации (и снизить значение коэффициента чувствительности В₄), если на операции (3, 4) осуществлять контроль данных после их исправления. Графическая модель информационной цепи, соответствующая данной организации процесса переработки информации, приведена на рис.5.11,б.

Возможность снижения вероятности ошибок до значения Q_доп.  определим при числе циклов контроля k à ∞ (при q_j << 1 для всех j).

В соответствии с формулой (2.32) имеем:

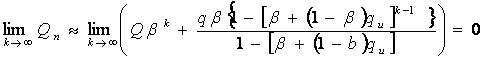  (2.33)

 Учитывая, что в данном случае

q_и=q₃   ,q=1- (1 – q₁ )(1 – q₂)≈q₁+q₂, Q₃≈Q_bx+q₁+q₂,

находим максимальное число циклов контроля, при которых Q₄ =Q_доп. Последовательно подставляя в формулу (5.5) значения k =2,3,…, находим, что при k =2 Q₄=2∙10^-5>Q_доп., при k=3 Q₄=3,2∙10^-6<Q_доп.

     Таким образом, при k=3 обеспечивается предельно допустимое значение показателя безошибочности информации.

Задача 2.8. Для совершенствования условий хранения дисков в архивах предприятий предусматривается провести сбор и обработку статистических данных о сохранности (надежности сохранения) информации на дисках в период их эксплуатации и хранения. С этой целью осуществляется выборочный контроль информации при объеме выборки n=90Мбайт, что составляет долю v = 0.06 от общего объема информации. При обнаружении хотя бы одной ошибки в выборке проверяется весь объем информации с исправлением обнаруженных ошибок. Вероятность пропуска ошибки при контроле информации, записанной на дисках, пренебрежимо мала.

Оценить безошибочность информации на дисках после проведения выборочного контроля, считая, что до его проведения вероятность наличия ошибок в одном байте информации Q=1∙10^-9.

Р е ш е н и е. Согласно методике оценки безошибочности информации при выборочном контроле математическое ожидание доли ошибок в общем объеме принятой информации («средний выходной уровень дефектности информации»)

q_в=M_в/N=QL(Q).          (2.34)

Вероятность L(Q) зависит от закона распределения случайной величины – числа ошибок в выборке. При объеме выборки n <0,1N и Qn<0,1 можно использовать распределение Пуассона с параметром a=nQ. При этом

q_в=Q_exp(-nQ).                 (2.35)