Расчёт апроксимирующей передаточной функции объекта для заданной динамической характеристики объекта управления, страница 7

8) Определяем интегральные площади:

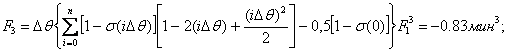
9) Выбираем структуру передаточной функции. Так как в момент времени t=0, h(0)=h^’(0)=h^’’(0)=0 и F₃<0, то передаточную функцию выбираем вида

(1.3.1)

где a₁=F₁=5.39 мин;

a₂=F₂=7.87 мин²;

k=h(¥)/Dx_2вх=20/1=20;

Тогда передаточная функция исследуемого объекта W_об(p) будет иметь окончательный вид:

(1.3.2)

График переходной характеристики полученной передаточной функции при x_вх=1 представлен на рис.1.3.4.

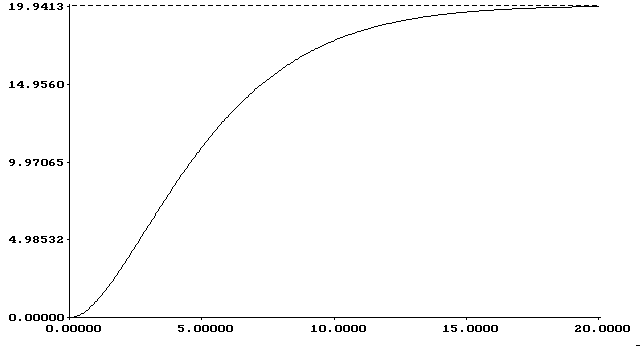
рис.1.3.4 Переходная характеристика полученной передаточной функции

Определяем точность полученных расчетов по данному методу.

Для передаточной функции второго порядка апериодического звена переходную характеристику можно найти по формуле при T₁>T₂:

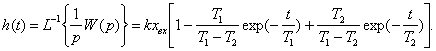(1.3.3)

Тогда для нашей полученной передаточной функции формула (1.3.3) при x_вх=1 примет вид (T₁>T₂):

(1.3.4)

В таблице 1.3.3 сведены экспериментальные и полученные значения переходной характеристики.

Таблица 1.3.3