Расчёт апроксимирующей передаточной функции объекта для заданной динамической характеристики объекта управления

1. РАСЧЁТ АПРОКСИМИРУЮЩЕЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ОБЪЕКТА

ДЛЯ ЗАДАННОЙ ДИНАМИЧЕСКОЙ ХАРАКТЕРИСТИКИ ОБЪЕКТА

УПРАВЛЕНИЯ

Для заданной динамической характеристики (кривой разгона) объекта управления, изображенной на рис.1.1, рассчитаем аппроксимирующую функцию объекта тремя методами.

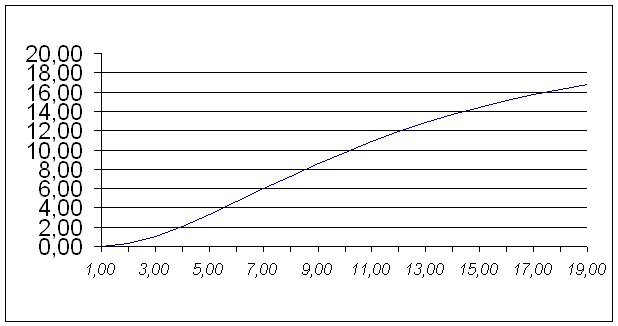Рис. 1.1. Кривая разгона объекта управления

1.1.  Расчет аппроксимирующей передаточной функции объекта  апериодическим звеном первого порядка

Свойства сложных объектов, которые описываются переходными процессами могут быть найдены экспериментально. На практике эти объекты заменяются объектами первого порядка с запаздыванием. Тогда уравнение динамики будет иметь вид:

                                   (1.1.1)

      где: y - регулируемая величина;

             x - регулирующее воздействие;

             T - условная постоянная времени объекта;

             k - коэффициент передачи объекта;

            t - время запаздывания астатического объекта;

              t - время; 

T

t

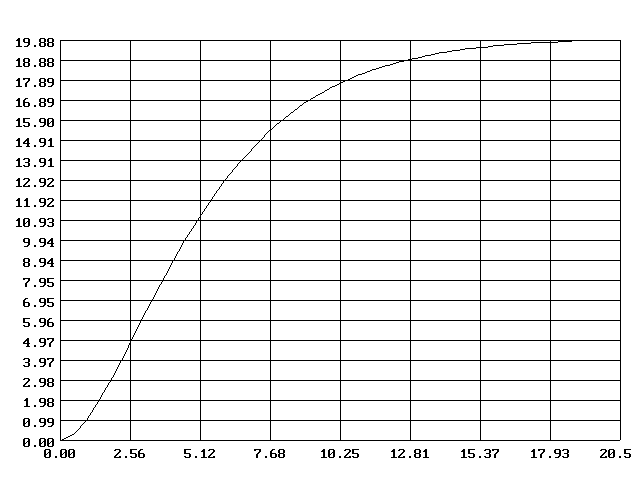
рис.1.1.1 Экспериментальная разгонная кривая

Для определения передаточной функции проводим касательную в точке перегиба и определяем участок запаздывания t=0.9 мин. Проводим линию параллельную временной оси через точку на оси ординат равной 0.63×h_уст=12.6 и находим t^*=5.9 мин. Определяем постоянную времени объекта как T=t^*-t=5.9-0.9=5.0 мин.

Таким образом в результате расчетов была получена передаточная функция следующего вида при x_вх=1:

                                                  (1.1.2)

График полученной аппроксимирующей функции представлен на рис.1.1.2

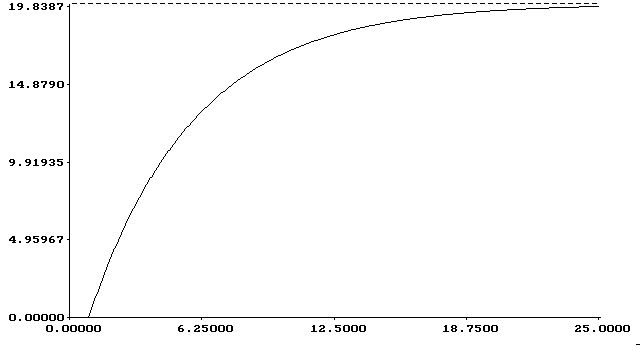
рис. 1.1.2. Разгонная переходная характеристика аппроксимирующей

 передаточной функции

Точность полученных расчетов можно определить по формуле:

 =                                             (1.1.3)

где   - значение характеристики , полученного в ходе эксперимента ;

        -  значение характеристики, полученной в ходе аппроксимации.

Теоретическое значение выходного сигнала можно получить , используя преобразование Лапласа и формулы разложения .