Расчёт апроксимирующей передаточной функции объекта для заданной динамической характеристики объекта управления, страница 11

Проверяем ПИ-регулятор на максимальное отклонение.

    По рис.4 методического приложения «Инженерные методы выбора типа автоматического регулятора» определяем R_д=0,3.

По формуле (2.4) находим y₁=R_дk₀x_в=1*20*0.3=6

По условию (2.3) проверяем подходит ли нам ПИ-регулятор.

y₁=6 £y_1.доп=7

Так как условие выполняется, следовательно ПИ-регулятор подходит.

          Проверяем ПИ-регулятор на время переходного процесса.

          По рис.9 методического приложения «Инженерные методы выбора типа автоматического регулятора» приt₀/Т₀=0.18 определяем t_р/t₀=8.

Следовательно t_р=8*0.9= 7.2 мин.

По условию (2.7) проверяем подходит ли нам ПИ-регулятор на время переходного процесса.

t_р=7.2<t_1.доп=15.

Так как условие выполняется, следовательно, для объекта выбираем ПИ-регулятор.

3. РАСЧЕТ НАСТРОЕЧНЫХ ПАРАМЕТРОВ РЕГУЛЯТОРА

Расчет настроечных параметров производится методом расширенных АФЧХ.

Метод Расширенных АФЧХ базируется на:

- использовании в качестве критерия, определяющего качества переходного процесса регулирования - степень затухания y.

- определении расширенных амплитудно-фазовых характеристик объекта и регулятора;

- применении основного условия устойчивости замкнутой системы;

Определим настроечные параметры регулятора.

Передаточная функция объекта:

                                                                                         (3.1)

   где  k=20 ;

t=0  мин;

           a₀=1;

           a₁=5.39 мин;

           a₂=7.87 мин²;

Закон регулирования ПИ.

1. Записываем передаточную функцию ПИ-регулятора

                                                                                                           (3.2)

    2. Используя условие

W_об(p)×W_р-1=0 ,                                                  (3.3)

и подставляя значения передаточных функций в условие (3.3), получим:

,

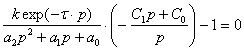                                      ,                         (3.4)

     3. При построении области устойчивости необходимо в уравнении (3.4) провести замену p=-mw+jw.

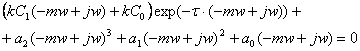
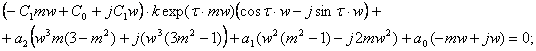
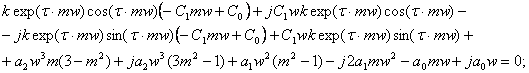
      Разделим вещественную и мнимую части и приравняем их порознь к нулю:

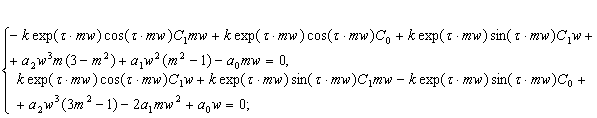
     4. Решая эту систему уравнений, находим:

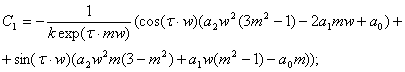
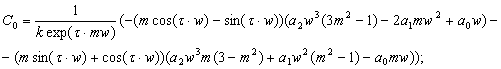
5. Подставляем последовательно в выражения для нахождения С₀ и С₁ численные значения w и m, результаты сводим в таблицы и строим график зависимости С₀=f(C₁) и находим оптимальные настройки.