Лабораторний практикум з курсу “Теорія автоматичного управління”: Навчальний посібник, страница 19

    2.7. Використовуючи програму ASYMPTOTE побудувати графіки LАЧХ,LФЧХ і ассимтотическую LАЧХ G5(S). Розрахувати аналітично і побудувати графік ассимтотической LАЧХ і порівняти з отриманою характеристикою.

ІІІ. Контрольні питання

3.1. Перелічити частотні характеристики ланок.

3.2. Який зв'язок між частотними характеристиками?

3.3. Який зв'язок між частотними і тимчасовими характеристиками?

3.4. Як змінюються частотні характеристики при зміні параметрів ланок?

3.5. Що характеризують частотні характеристики?

3.6. Пояснити методи побудови частотних характеристик.

3.7. Пояснити методи експериментального визначення частотних характеристик.

3.8. Які переваги має логарифмічний спосіб побудови частотних характеристик ?

3.9. Пояснити розходження між мінімально-фазовими не мінімально фазовими ланками.

3.10. З якою метою введене поняття логарифмічних частотних характеристик.

3.11. Які одиниці виміру застосовують для логарифмічних амплітудних і фазових характеристик ?

Таблиця 1

N в	G1(S)	G2(S)	G3(S)	G4(S)	G5(S)
	Інтегр.	апеp.	колив.	два апер.	з’єднання
1	T=0.1c	K=0.1 T=0.c	K=1 T=0.2c D=0.2	K1=1 T1=0.2c K2=0.5 T2=0.5c
2	T=0.2с	K=0.2 T=0.7c	K=1 T=0.1c D=0.4	K1=0.1 T1=0.2c K2=0.2 T2=0.5c
3	T=0.3c	K=0.3 T=0.6c	K=1 T=0.2c D=0.1	K1=1 T1=1c K2=1 T2=2c
4	T=0.4c	K=0.4 T=0.5C	K=1 T=0.4c D=0.4	K1=1 T1=1c K2=2.5 T2=1c
5	T=0.5c	K=0.5 T=0.4c	K=1 T=0.5c D=0.5	K1=2 T1=1c K2=5 T2=1c
6	T=0.6	K=0.6 T=0.3c	K=1 T=0.2c D=0.4	K1=1 T1=0.2c K2=5 T2=0.5c
7	T=0.7c	K=0.7 T=0.2c	K=1 T=0.4c D=0.2	K1=2 T1=1c K2=5 T2=0.1c
8	T=0.8c	K=0.8 T=0.1c	K=1 T=0.5c D=0.4	K1=1 T1=0.5c K2=2 T2=0.2c

ЛАБОРАТОРНА РОБОТА №10

Тема: Дослідження стійкості дискретної САУ.

Мета: Вивчення критеріїв стійкості. Освоєння методики дос-лідження стійкості дискретної  САУ на ПЭВМ із використанням пакетів моделювання.

                     І. Методичні вказівки по виконанню роботи

    2.1.  Для того, щоб дискретна САУ була стійка, необххідно і досить, щоб дійсні частини всіх коренів характеристичного  поліному САУ були відємні та  розташовані в межах основної смуги, тобто

 Для характеристичного рівняння у формі Z-перетворення умова стійкості має вигляд:

 Розглянемо систему, структурна схема якої зображена на мал. 10.1 та визначимо її стійкість.

 

                     -

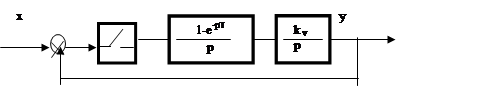Рис.10.1

    Передатна функція розімкнутої системи

.

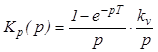    Передатна функція розімкнутої дискретної системи

.

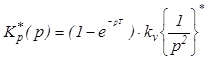    Передатна функція розімкнутої дискретної системи у формі z- перетворення

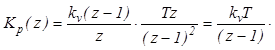
      Передатна функція замкнутої дискретної системи у формі z - перетворення

 .

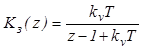      Характеристичне рівняння                

Умова стійкості визначається співвідношенням :

      Критичний коефіцієнт підсилення визначається залежністю :

Для аналізу стійкості  дискретних систем у пакеті СС використовується програма STABІLІTY, при цьому вихідні дані задаються у виді передаточної функції розімкнутої системи.

  Запис:   DІG > STAB, G11 ¿

        Результатом виконання програми є :

         - структурна схема замкнутої системи;

         - характеристичний поліном;

         - значення коренів характеристичного рівняння;

         - висновок про стійкість системи.

Програма ROUTM - дозволяє визначити область стійкості при зміні коефіцієнта підсилення розімкнутого контуру.

 Запис:   DІG > ROU, G11 ¿

 Результатом виконання програми є :

   - структурна схема замкнутої системи;