Система автоматического регулирования уровня воды в диаэраторе ДСА-300 в электрокотельной «Энергетик» на ТЭЦ-7 г.Братска, страница 9

Точка где h’(t)-максимальная является точкой перегиба, т.е. в данном

случае это точка при tр=3 мин.

2) Далее строится нормированная переходная характеристика h”(t) и через

точку перегиба tр проводится касательная к ней (рис.2.5).

3) Находим отрезки a и b, а также отношение a/b. Имеем a=8,6 и b=10,8.

Тогда отношение (a/b) = 0,796 ≈ 0,8.

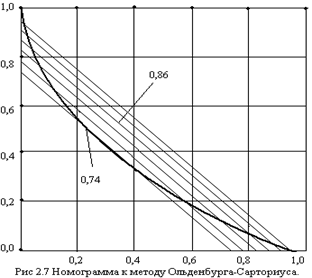
4) Затем воспользуемся номограммой, изображенной на рис.2.7 и отложим

точку 0,8 по обеим осям номограммы.

5) Концы отрезков соединим прямой линией, которая пересечёт номограмму

в двух точках на расстоянии A и B. A=0,157; B=0,793.

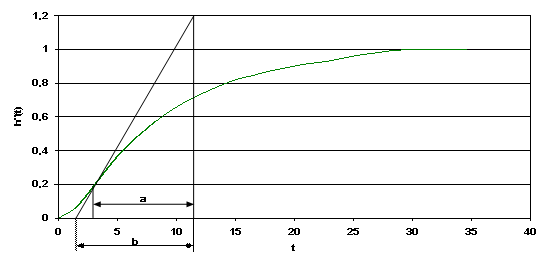
Рис.2.5. Нормированная переходная характеристика

6) Найдём постоянные времени:

T₁=B*b=0,793*10,8=8,56 мин;

T₂=A*a=0,157*8,6=1,35 мин.

7) Определим расчётную точку перегиба:

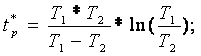
t_p*=2,96 мин.

8) Найдём время полного запаздывания: t=t_p-t_p*

t=3-2,96=0,04 мин.

Передаточная функция будет выглядеть следующим образом:

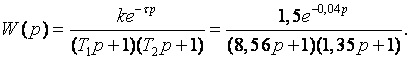
9) Получим и построим расчётную переходную характеристику объекта :

h(t)=1,5+0,281*exp(-0,741(t-0,04))-1,78*exp(-0,117(t-0,04)).

10) Определим ошибку аппроксимации:

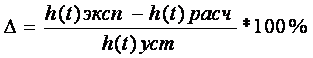
Ошибка аппроксимации - |D_max|=2,9 %, исходя из ниже приведённой таблицы.

Таблица 2.4