Величина g характеризующая интенсивность затухающего процесса, численно равна абсолютному значению действительной части корня характеристического уравнения, это называется степенью устойчивости переходного процесса.
Степень колебательности переходного процесса m характеризует затухание его колебательных составляющих и численно равна абсолютному значению отношения действительной части к коэффициенту при мнимой части корня характеристического уравнения с наименьшим абсолютным значением этого отношения.
Степенью затухания y называют отношение разности двух соседних амплитуд к первой из них. Ее можно выразить через степень колебательности процесса:
y = 1- е-2mp,
где 2pm – логарифмический декремент затухания колебаний.
tg g = m, т.е. получаем, что g = arctg m
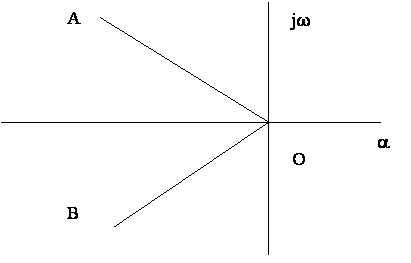 |
Рис. 4.3. К раскрытию понятия РАФЧХ
Степень затухания рассматриваемой составляющей процесса будет определяться значением тангенса этого угла. Если корень характеристического уравнения этой системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания y будет постоянной.
Выражение передаточной функции звеньев, для которых рк находится на линии АОВ, называется расширенной АФЧХ:
W(m, jw)=A(m, jw)*(e-j(m, jw))
Если m=0, то РАФЧХ совпадает с линией АОВ и совмещается с мнимой осью, следовательно, АОВ – мнимая ось, а система находится на границе устойчивости. При расчете системы используется соотношение:
W(m, jw)об.*W(m, jw)р=1 (1)
Если корень характеристического уравнения системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания y будет одна и та же.
Передаточная функция объекта, найденная при помощи самого точного метода:
![]()
Выбран ПИ-закон регулирования с передаточной функцией:
Wp(p)=
![]()
Для получения РАФЧХ объекта произведём замену p=-mw+jw в передаточной функции объекта и выделим реальную и мнимую части.
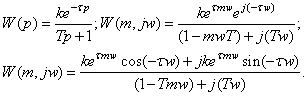
Умножим числитель и знаменатель на комплексно сопряжённое знаменателю число и выделим Re(w) и Im(w):
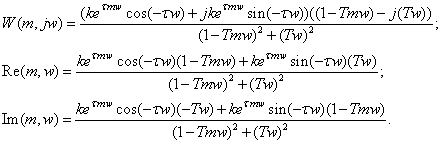
Произведём подстановку:
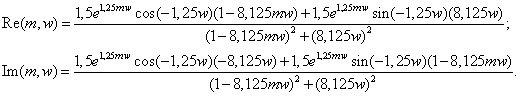
Для получения вещественной и мнимой характеристик регулятора воспользуемся следующими формулами:
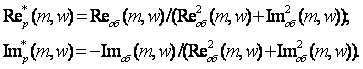
Для получения настроечных коэффициентов регулятора воспользуемся следующими формулами:
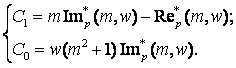
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.