Система автоматического регулирования уровня воды в диаэраторе ДСА-300 в электрокотельной «Энергетик» на ТЭЦ-7 г.Братска, страница 13

t/T_об=1,25/8,125=0,154. Хотя данное значение меньше 0.2 , лучше выбрать регулятор непрерывного действия, чем позиционный.

3.2.  Выбора закона регулирования

В соответствии с технологическими требованиями в нашем случае не допускается 20 % -ое перерегулирование, поэтому выбираем апериодический переходный процесс без перерегулирования .

Время регулирования примем равным приблизительно  t_p=20 минутам.

Используя номограмму и значения t/T_об=0,154 и t_p/t=16 определим закон регулирования. Используем для рассмотрения рис.3.1 а). По оси абсцисс отложим значение 0,154 , а по оси ординат – 16. Получим точку 1, которая означает, что нужно применить ПИ-закон регулирования.

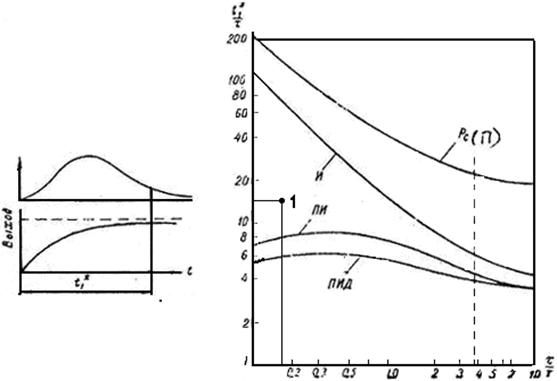
Рис. 3.1.   Номограмма к определению закона регулирования.

 

4.  Определение настроечных параметров регулятора

 

4.1.  Табличный способ

В данной работе мы рассматриваем апериодический переходный процесс без перерегулирования. Ранее выбрали ПИ-закон регулирования.

Из метода аппроксимации, который дал результат с меньшей ошибкой (графо-аналитический метод ), получили следующие параметры объекта k_об=1,5; t=1,25 мин; T=8,125 мин.

С помощью табличных формул получаем k_p, T_и.

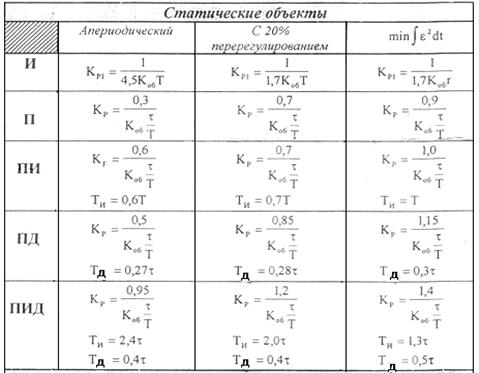
Рис. 4.1.  К определению настроечных параметров регулятора табличным методом.

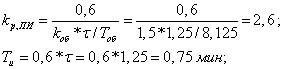
Отсюда: С₀=k_p/T_и=3,47; C₁=k_p=2,6

Определим передаточную функцию замкнутой системы :

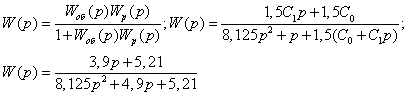
Определим выражение для сигнала на выходе системы:

h(t)= 1,5+1,543*exp(-0,3t)*cos(0,742t+3,376)

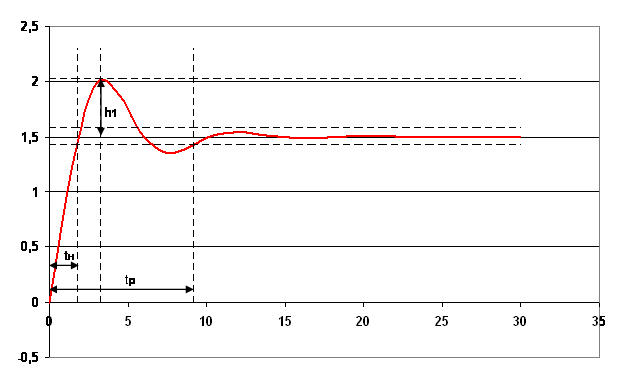Рис.4.2.   Переходный процесс с настроечными параметрами регулятора Со=3,47 ; С1=2,6

Определим интегральную оценку качества переходного процесса:

 I=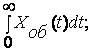

I = ∫ | h(t)-h_уст | dt =  | h(i∙∆t)- h_уст | ∙∆t =32,58 ·0,1=3,258

Определим показатели качества получившегося переходного процесса.

1) Время переходного процесса t_p=9,2 мин;

2) Перерегулирование s=(h_max-h_уст)/h_уст=(2,02-1,5)/1,5=34,7%;

3) Число колебаний 1;

4) Колебательность d=h₂/h₁*100%=0%;

5) Частота колебаний для данного процесса не определяется;

6) Время достижения первого максимума t_max=3,3 мин;

7) Время нарастания переходного процесса t_н=1,87 мин;

8) Степень затухания y=(А_i-A_i+2)/A_i=0.

4.2.  Метод расширенных АФЧХ

Для условия устойчивости необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательные вещественные части.

Если все корни характеристического уравнения лежат левее некоторой прямой, проведенной в левой полуплоскости параллельно мнимой оси на расстоянии g от нее, то система обладает некоторой степенью устойчивости.