Модернизация системы автоматики с помощьюя современных средств автоматизации, страница 7

Продолжение таблицы 2.2.

Из таблицы и рисунка видно, что погрешность  превосходит допустимую погрешность в 5% и равна 10,62 %. Отсюда делаем вывод, что выбранный метод аппроксимации не подходит для данной передаточной функции.

2.2 Метод Ольденбурга-Сарториуса.

В данном методе передаточная функция будет иметь вид:

.

    1.Этот метод требует нормирования экспериментальной переходной характеристики в виде   графика (рис. 2.5.) и таблицы 2.3.

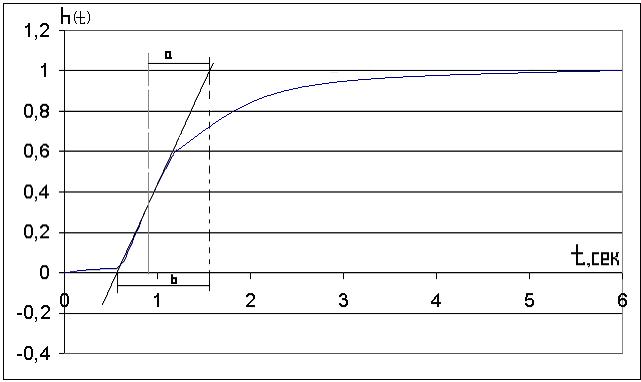
Рисунок 2.5.  Экспериментальная нормированная характеристика.

   2.Точку перегиба привести к нормированному значению и отметить на графике переходного   процесса. Определяем точку перегиба экспериментальной характеристики:

       h’(t) = h_i+1(t) – h_i(t).  

                                                 Таблица 2.3.