Управление качеством переходных процессов в многосвязных системах. Методические указания к выполнению курсового проекта

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО «Братский государственный университет»

                                                                                                                    А.Н. Дойников

УПРАВЛЕНИЕ КАЧЕСТВОМ ПЕРЕХОДНЫХ ПРОЦЕССОВ В МНОГОСВЯЗНЫХ СИСТЕМАХ

Методические указания к выполнению курсового проекта

Братск 2006г.

1. ЗАДАНИЕ НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

1.1.  Используя схему электроэнергетической системы и результирующие данные курсового проектирования по дисциплине “Переходные процессы в электрических системах”, составить эквивалентную простейшую электрическую систему (“электропередачу”) (рис.1.1).

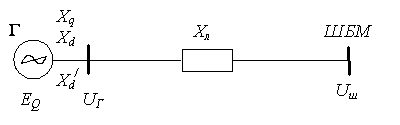
Рис.1.1. Простейшая электрическая система

1.2. Используя дополнительные данные индивидуального задания (, , , , , , , , ) (табл.1) и соотношения (2.1-2.21),  рассчитать аналитически режим работы электропередачи, оформив результаты в виде пяти «Строк- таблиц» (табл. 3 – 6).

1.3. Построить угловую характеристику активной мощности и определить коэффициент запаса апериодической устойчивости (рис1.3, соотношение 4.32).

1.4.  Составить дифференциальные уравнения движения Горева-Парка для электромеханических процессов (п.4) и линеаризовать их в виде (4.46) в точке рассчитанного режима.

1.5.  Рассчитать аналитически частные производные по параметрам регулирования: , _, , _, ,  соотношения (4.57-4.58 и 5.80-5.83).

1.6. Используя значения частных производных, составить характеристический определитель (ХО), характеристический полином (ХП) (4.53) и передаточные функции (ПФ) параметров регулирования разомкнутой системы: ,  (4.54-4.56)_.  Определить корни характеристического полинома. Сделать выводы по статической устойчивости системы. Используя (4.54-4.56), рассчитать две особые точки ЧХ на «нулевой» и «резонансной» частотах.

1.7. Используя исходные данные варианта (табл.2), составить передаточные функции каналов регулирования:

.

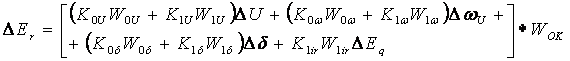1.8. Используя значения частных производных, соотношения (5.62, 5.79) составить характеристический определитель (ХО), характеристический полином (ХП) и передаточные функции (ПФ) параметров регулирования замкнутой системы: , . Определить корни ХП при заданных значениях коэффициентов регулятора.

1.9. Рассчитать аналитически особые точки (для нулевой и резонансной частоты) ЧХ замкнутой системы (используя 5.79) и кривой Д-разбиения (области устойчивости). Варьируя коэффициенты ,  относительно граничных значений, показать достоверность построенной области устойчивости.

1.10. Выполнить контрольные расчеты режима, угловой характеристики, частотных характеристик и областей устойчивости с использованием программы MACHIN (рис.1.2-1.5).