Управление качеством переходных процессов в многосвязных системах. Методические указания к выполнению курсового проекта, страница 9

В (4.34) исключим  с помощью (4.26)

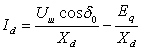.                                                                                 (4.36)

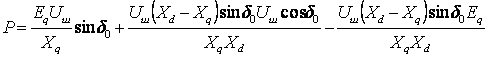.           (4.37)

Таким образом:

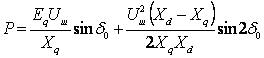.                                                        (4.38)

В уравнении (4.38) , то есть . Поэтому линеаризованное уравнение принимает вид:

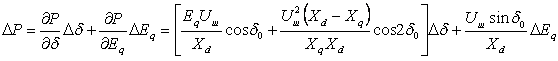.    (4.39)

Исключим из (4.28) , используя (4.26):

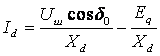.                                                                             (4.40)

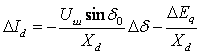.                                                                     (4.41)

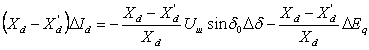.                                   (4.42)

Тогда уравнение (4.28) примет вид:

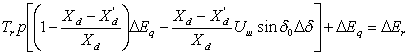.                           (4.43)

Обозначим:

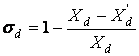.                                                                                 (4.44)

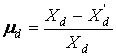.                                                                                      (4.45)

Таким образом, система двух линеаризованных уравнений с двумя неизвестными примет вид:

.                                                       (4.46)

Положим, что к обмотке возбуждения генератора приложено гармоническое возмущение  с амплитудой  и частотой . Тогда изменение переменных  и  также будет гармоническим.

При переходе к комплексным амплитудам и частотному изображению система (4.46) примет вид:

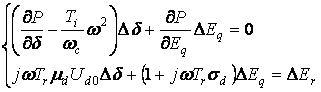.                                             (4.47)

Обозначим:

.             .                                        (4.48)

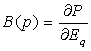.                       .                                               (4.49)

.        .                                   (4.50)

.                .                                         (4.51)

Тогда исходную систему дифференциальных уравнений  можно представить в матричном виде:

.                                                                    (4.52)

Свободный определитель данной системы является общим знаменателем для всех передаточных функций и может быть записан в виде характеристического полинома:

.                                                              (4.53)

При этом полином имеет корни, характеризующие общие динамические свойства, в том числе и статическую устойчивость системы. В исследуемом случае электромеханического движения знаменатель  3^го порядка, имеет одну комплексную пару корней и один действительный корень.