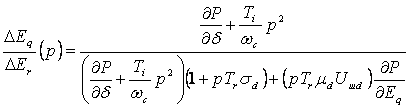Управление качеством переходных процессов в многосвязных системах. Методические указания к выполнению курсового проекта, страница 15

.                              (7.97)

Тогда в соответствии с формулой Мейсона (7.88) можно составить передаточную функцию многоконтурной замкнутой системы (рис.7.8) в виде отношения операторных выражений для числителя и знаменателя:

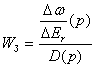.                                                                                                     (7.98)

Знаменатель D(p) вычисляется по (7.89) и является выражением для характеристического определителя, общего для передаточной функции по любому параметру стабилизации в системе (Dδ,DE_q,DU или Dw):                                                                                            

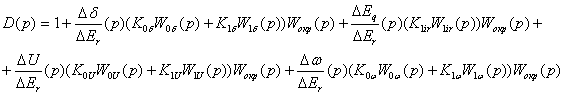 .        (7.99)

Числитель функции (7.98) записывается как передаточная функция прямого пути по одному из используемых в регуляторе параметру стабилизации. В рассматриваемом случае (при выделении в качестве оптимизируемого канала регулирования по отклонению частоты  и ее производной) числитель формируется в виде: . Заметим, что при выделении в качестве оптимизируемого канала по отклонению электрического угла и его производной числитель бы формировался передаточной функцией соответствующего прямого пути: . В последнем случае передаточная функция замкнутой по всем каналам системы W_З(p), сформированная по соотношению аналогичному (7.98)

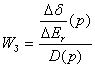  полностью соответствует передаточной функции замкнутой системы W_З(p), сформированной в предыдущем параграфе (5.79) при несколько другом подходе.

Возвращаясь к методике построения кривых Д- разбиения в плоскости двух выделенных коэффициентов регулирования, необходимо операторное выражение для характеристического знаменателя (7.99) переписать упрощенно, оставляя в явном виде подробное описание лишь выделенных для оптимизации каналов регулирования. В частности, в нашем случае, при построении границы устойчивости и кривых равного качества в плоскости двух коэффициентов (w_k,K_0w,K_1w) выражение для характеристического полинома (7.99) можно представить в виде:

     (7.100)

В выражении (7.100) передаточные функции замкнутых контуров регулирования  

                                                (7.101)

                                                                 (7.102)

,                                              (7.103)

являются известными при заданных коэффициентах и постоянных времени регулирования (5.59-5.61). В курсовом проекте указанные параметры задаются таблицей 2 исходных данных. Передаточные функции прямых путей (разомкнутой системы) также известны. Соотношения для  и получены выше (7.96-7.97) , а выражение для  строится на их основе (7.94), что с подтверждается структурной схемой (7.8).

С учетом того, что в исследуемом, разомкнутом контуре регулирования передаточные функции прямого пути  (7.95) и передаточные функции звеньев канала регулирования из табл.2 и выражений (5.59-5.61) также известны, можно перейти к окончательной форме полинома в соответствии с (7.85):