Управление качеством переходных процессов в многосвязных системах. Методические указания к выполнению курсового проекта, страница 13

 .                                    (6.86)

Семейство решений данной системы в виде (w_k,K_0w,K_1w) образует совокупность точек границы устойчивости или кривой Д-разбиения в плоскости двух выбранных параметров. Пример такой кривой приведен на рис.1.5. Напомним, что все точки плоскости (комбинации пар коэффициентов), расположенные левее границы, при перемещении по ней в направлении увеличения расчетной частоты, определяют область устойчивости. И наоборот, любая комбинация коэффициентов, выбранная правее границы приводит к потере устойчивости системы, т.е. к приобретению правой пары корней.

Можно заметить, что замена в выражении (6.85) p=a_з+jw приведет к построению годографа и кривых Д- разбиения, отражающих не границу устойчивости, а некоторые кривые, смещенные относительно границы во внутрь области устойчивости на заданную величину a_з. Последнее соответствует поиску условий (комбинаций коэффициентов регулятора) для расположения корней на комплексной плоскости на оси, смещенной влево от начала координат на величину a_з (рис.6.7).

Рис.6.7. Вывод пары комплексных корней с мнимой частью jw=jw_k  с помощью найденной комбинации коэффициентов (w_k,K_0w,K_1w) на границу устойчивости (ось “j”) и на ось равной степени устойчивости (“a_з+j”)

Для пояснения методики проведем следующие структурные преобразования.

Вначале представим принципиальную схему АРВ-СД (рис.6.4) структурно таким образом, чтобы в ней в явном виде присутствовали коэффициенты усиления и передаточные функции по всем каналам регулирования (рис.6.7), в соответствии с (5.62).

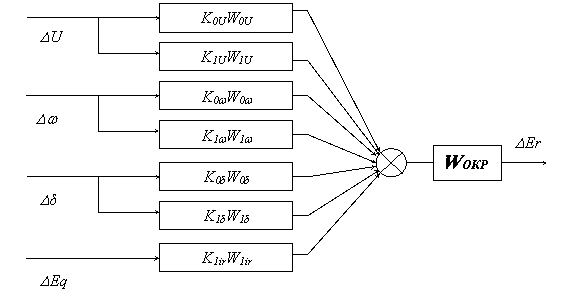
Рис. 6.7. Структурная схема АРВ-СД

Затем структурную схему замкнутой по всем каналам системы (рис.6.5.) более подробно раскроем с учетом схемы АРВ-СД (рис.6.7) и соотношений (5.62, 5.68,5.69). Заметим, что на рис 6.5,6.7 и 6.8 для сокращения в обозначениях передаточных функций опущен оператор «p».

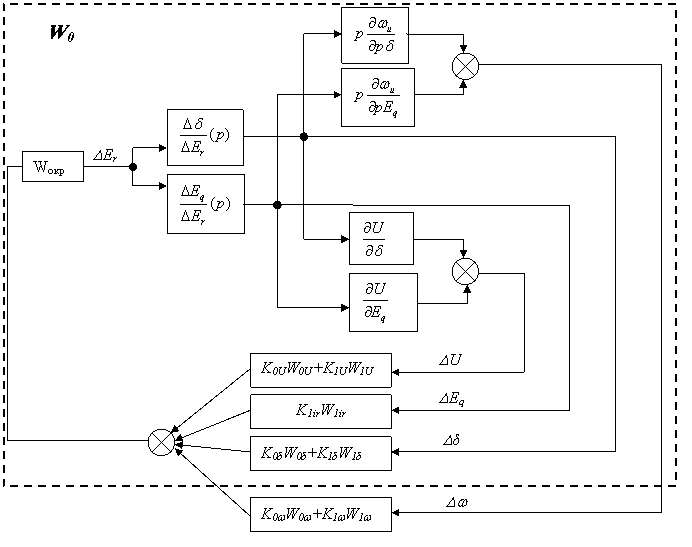
Рис. 6.8. Структурная схема системы, замкнутой по всем каналам регулирования

Пунктирной линией на рис.6.8. выделена структура упомянутой выше обобщенной передаточной функции (p). Нетрудно видеть, что при ее использовании структурная схема, представленная на рис.6.8 трансформируется в одноконтурную (рис.6.6.).  Искомая ПФ может быть рассчитана по известным функциям элементов и звеньев, входящих в (p).

В практических задачах оптимизации настроечных параметров регуляторов часто используется экспериментальная АФЧХ ((jw)) реальной системы с рабочими коэффициентами усиления по всем каналам регулирования и разомкнутой лишь по исследуемому каналу. При наличии такой ЧХ отпадает необходимость в трудоемких расчетах соответствующей обобщенной ПФ (p) и последующем переходе к ее частотному изображению. В этом случае процедура построения границы устойчивости начинается непосредственно с использования соотношения (6.85).