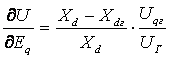Управление качеством переходных процессов в многосвязных системах. Методические указания к выполнению курсового проекта, страница 12

.                                                                           (5.81)

.                                                      (5.82)

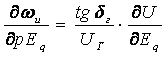.                                                                            (5.83)

Выражение (5.79) является частотной характеристикой замкнутой системы, представленной на рис. 5.5.

Выражения (4.55), (4.56), (5.79) служат основой для построения алгоритма расчета частотных характеристик регулируемой АРВ-СД простейшей электрической системы вида: генератор – внешняя реактивность – шины бесконечной мощности.

6. ПОСТРОЕНИЕ КРИВЫХ  Д- РАЗБИЕНИЯ В ПЛОСКОСТИ ДВУХ НАСТРОЕЧНЫХ КОЭФФИЦИЕНТОВ АРВ-СД

Для построения границы  устойчивости в плоскости двух параметров регулятора необходимо структурно представить описание системы в виде обобщенной передаточной функции , составленной относительно лишь двух, выделенных для исследования и оптимизации каналов (коэффициентов усиления по ним) регулирования. Остальные каналы должны иметь известное математическое описание (передаточные функции звеньев и фиксированные значения настроечных параметров), которое включено в  . В этом случае представляет собой ПФ системы,  разомкнутой только по выделенным каналам. Например, при построении кривых Д-разбиения в плоскости коэффициентов по каналам отклонения частоты (К_0w) и производной этого отклонения (К_1w), искомая структурная схема имеет вид, представленный на рис. 6.6.

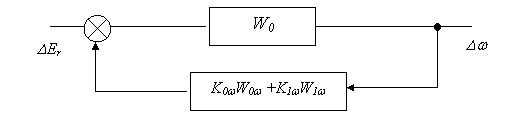
Рис. 6.6. Одноконтурная  структурная схема многоконтурной системы регулирования

По полученным передаточным функциям разомкнутой системы и выделенного канала регулирования строится характеристический полином, который является знаменателем соответствующей передаточной функции замкнутой системы

,                            (6.84)

где  - обобщенная ПФ системы,  разомкнутой только по выделенным каналам;  , - передаточные функции звеньев каналов регулирования по отклонению и производной отклонения частоты напряжения шин в соответствии с соотношениями (5.59 и 5.60).

Перейдя к частотным изображениям заменой   p=jw , из знаменателя (6.84) может быть получен характеристический годограф (годограф Михайлова), содержащий в явном виде исследуемые настроечные коэффициенты по каналам регулирования:

.                                   (6.85)

Для того, чтобы определить, значения К_0w и К_1w  , которые на текущей (расчетной) частоте w_k=2pf_k  сдвигают годограф Михайлова в начало координат, т.е. выводят систему на границу устойчивости D(jw_k,K_0w,K_1w)=0, необходимо для каждого заданного значения частоты w_k  решить относительно искомых двух коэффициентов два уравнения, обеспечивающие равенство нулю действительной и мнимой части выражения для характеристического годографа: