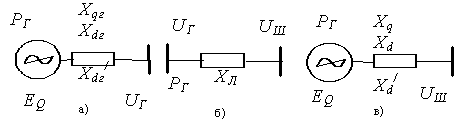
Рис.3.3. Расчетные участки последовательной цепи: генератор (а), линия (б), система (с)
4. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ПАРАМЕТРОВ РЕЖИМА БЕЗ УЧЕТА ДЕЙСТВИЯ АРВ–СД
Частотные характеристики - это амплитудно-фазовые соотношения приращений параметров режима при задании гармонического возмущения на обмотку возбуждения генератора. Эти характеристики целесообразно использовать при анализе границ колебательной устойчивости и взаимного влияния каналов регулирования по различным параметрам режима и их производным. Рассмотрим частотные характеристики электропередачи, включающей синхронный генератор, работающий через внешнюю реактивность на шины неизменного напряжения. Для изучения этих характеристик можно использовать соотношения, получаемые из решения линеаризованных уравнений Горева-Парка, которые используются для исследования переходных процессов. Не учитывая для простоты выкладок демпферные контуры и исключая составляющие, обусловленные быстрозатухающими переходными процессами и изменением скорости вращения ротора относительно синхронной оси, запишем уравнения в виде [1]:
![]() . (2.22)
. (2.22)
![]() . (4.23)
. (4.23)
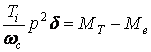 . (4.24)
. (4.24)
![]() . (4.25)
. (4.25)
В (4.24-4.25) и далее литера «p» используется как символ дифференцирования переменной по времени (не путать с литерой «P», обозначающей активную мощность генератора).
Линеаризованные уравнения переходных процессов электропередачи, работающей на мощную приемную систему запишутся в виде:
![]() . (4.26)
. (4.26)
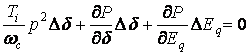 . (4.27)
. (4.27)
![]() , (4.28)
, (4.28)
где ![]() .
.
Уравнение движения в полных единицах:
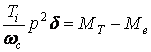 . (4.29)
. (4.29)
в относительных единицах ![]()
![]() . (4.30)
. (4.30)
Используя статорное
уравнение ![]() , имеем:
, имеем:
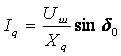 . (4.31)
. (4.31)
Необходимо привести уравнение (4.27) к базисным переменным. Тогда:
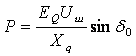 . (4.32)
. (4.32)
Поскольку линеаризовать
необходимо по ![]() , то распишем:
, то распишем:
![]() . (4.33)
. (4.33)
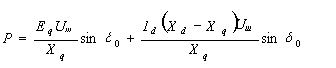 . (4.34)
. (4.34)
Уравнение движения ротора (4.29-4.30) примет следующий вид:
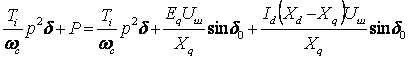 . (4.35)
. (4.35)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.